This is “Nucleus”, by Tim Locke, on display at the 2012 Bridges Math and Art Conference at Towson University.
Locke uses design technology (like CAD software), and manufacturing technology (like last-cut metal printing) to turn his line drawings into 3D sculptures.
You can learn more about Locke’s work here.
As part of my review of the 2012 August New York State Math Regents exams, I came upon this question, which rivals some of the worst I have seen on these tests. This is #11 from the Geometry exam.
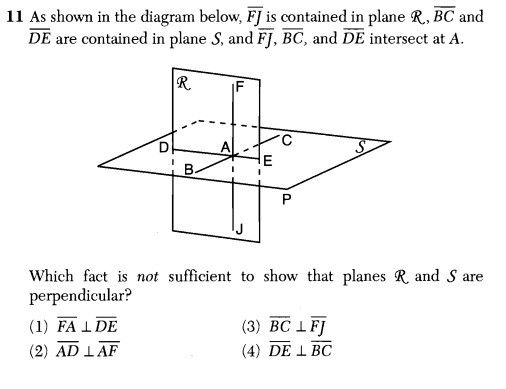
This question purports to be about knowing when we can conclude that two intersecting planes are perpendicular. Sadly, the writers, editors, and publishers responsible for this question clearly do not understand the mathematics of this situation.
Each of the answer choices is a statement about two lines in the given planes being perpendicular. The problem suggests that three of these statements provide sufficient information to conclude that the given planes are perpendicular. The student’s task is thus to identify which one of the four statements does not provide sufficient information to draw that conclusion.
There is a serious and substantial flaw in the reasoning that underlies this question:
Knowing that two lines are perpendicular could never be sufficient information to conclude that two containing planes are perpendicular.
In fact, given any two intersecting planes, you can always find two perpendicular lines contained therein, regardless of the nature of their intersection. A simple demonstration of this fact can be seen here. Thus, knowing that the planes contain a pair of perpendicular lines tells you nothing at all about how the planes intersect.
It’s not that this particular question has no correct answer; it’s that the suggestion that this question could have an answer demonstrates a total lack of understanding of the relevant mathematics.
How much does this matter? It’s a two-point question, it’s flawed, so we throw it out. No harm done, right?
Well, imagine a student taking this exam, whose grade for the entire year, or perhaps even their graduation, depends on the outcome of this test. Imagine the student encountering this problem, a problem that not only has no correct answer, but whose very statement is at odds with what is mathematically true. It’s not out of the realm of possibility that in struggling to understanding this erroneously-conceived question, a student might get rattled and lose confidence. Test anxiety is a well-known phenomenon. The effect of this problem may well extend past the two points.
Teachers are also affected. A teacher’s job may depend upon how students perform on these exams, but there isn’t any discussion about their validity. A completely erroneous question makes it through the writing, editing, and publishing process, and has an unknown affect on overall performance. After thousands of students have taken the exam, a quiet “correction” is issued, and the problem is erased from all public versions of the test.
What’s most troubling about this, to me, is that this is not an isolated incident. Year after year, problems like this appear on these exams. And when confronted with criticism, politicians, executives, and administrators dismiss these errors as “typos”, or “disagreements in notation.”
These aren’t typos. These aren’t disagreements about notation. These are mathematically flawed questions that appear on exams whose express purpose is to assess the mathematical knowledge of students and, indirectly, the ability of teachers to teach that knowledge. If the writers of these exams regularly demonstrate a lack of mathematical understanding, how can we use these exams to decide who deserves to pass, who deserves to graduate, and who deserves to keep their jobs?
Related Posts
This is “Skunks”, by Wouter Kersteman, on display at the 2012 Bridges Math and Art Conference at Towson University.
Read more about the artist and his work here.
Samuel Hansen has put together a wonderful podcast series, “Relatively Prime: Stories from the Mathematical Domain”, which offers engaging conversations about mathematics in action.
I am happy to have participated in the episode “1 + 1 = 2”, about the challenges facing mathematics education. The episode can be downloaded here:
http://relprime.com/oneplusoneequalstwo/
Samuel Hansen speaks with John Ewing, president of Math for America, as well as noted math educators Dan Meyer and Keith Devlin. In the segment on Math for America, I speak briefly about the positive impact this organization has had on my career.
I was proud to be able to represent MfA, and I am grateful to Samuel for letting me be a small part of this great project!
I was very happy with how well my piece “N Ways to Apply Algebra with the New York Times” has been received. Written for the New York Times Learning Network, this article was a response to this summer’s editorial “Is Algebra Necessary?”. My intention was to create opportunities for teachers and students to see and use algebra in the context of New York Times content and resources.
The piece generated a lot of comments, some of which I found quite surprising. For example,
This piece does an excellent job of demonstrating Mr. Hacker’s point – that algebra is unnecessary for most of daily life and work. Each of the above exercises is merely a more tedious and academic way of finding information that is readily available via the web or a simple calculator (link)
Naturally I disagree that the exercises are “tedious” and “academic”, but what really surprises me is the claim that if some piece of information is readily available via the web or calculator, then there’s no reason to teach it.
The commenter specifically refers to an activity which explores how various formulas govern housing prices, interest rates, and mortgage payments. While it is true that technologies exist that can calculate mortgage payments for us, students need more than just awareness of the existence of these formulas. House payments, car payments–debt payments in general–play a significant role in modern life. Students should explore the mathematics of these situations and develop experience, intuition, and understanding about the implications of that mathematics.
The above commenter agreed with an earlier comment:
These examples are pretty awful. No one would ever calculate mortgage payments using the actual formula. No one. (link)
Even if you believe no one would use the actual formula, how do calculators and computer programs find the answers for us? By using the actual formula.
I don’t like the suggestion here that it’s ok to tell students something like “It’s not important for you to know how mortgage payments are calculated; it’s good enough for you to know that someone else can do it for you.” This is wrong, both as a teaching matter (our goal should be to empower students) and as practical matter (are banks and mortgage lenders always trustworthy?).
Lastly, I found this comment both shocking and saddening:
I’m getting a PhD in Math Education. … I think the article pretty much proves that Algebra is not necessary. I am still, after many years, hoping to talk to someone other than an engineer who can give me an example of using Algebra in the workplace. As for using it in real life, I have never heard of it happening and I do not see it happening here. (link)
Someone earning a PhD in Math Education has no idea how anyone other than engineers use algebra in their jobs. And they proudly state that they have never heard of algebra being used in “real life”.
This is a purported expert in mathematics education, someone who, presumably, will be teaching and training future math teachers. And what will this person tell those future math teachers? That algebra isn’t necessary.