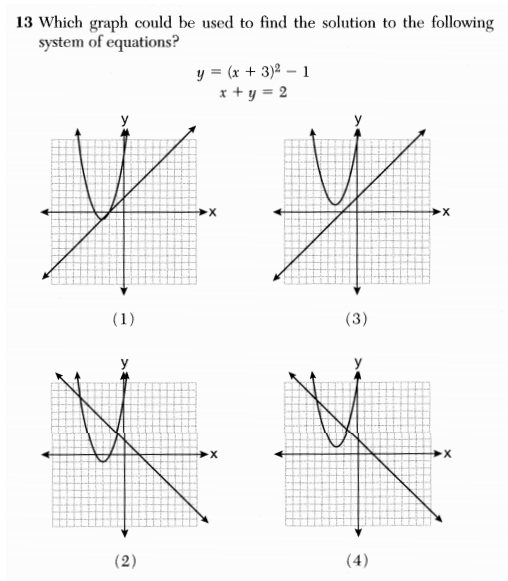
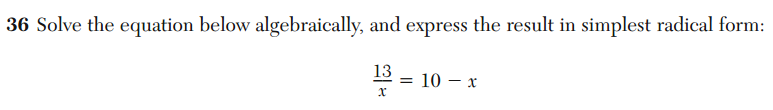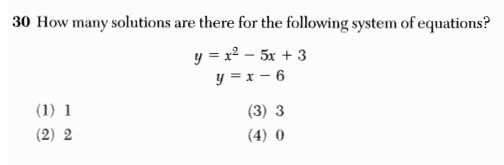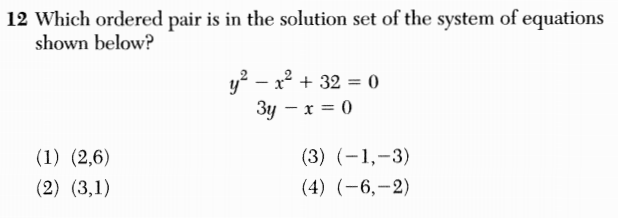I am very excited to be heading to Enschede, the Netherlands later this week for the 2013 Bridges conference!
I am very excited to be heading to Enschede, the Netherlands later this week for the 2013 Bridges conference!
The Bridges organization has been hosting this international conference highlighting the connections between art, mathematics, and computer science for the past 15 years. I have attended several Bridges conferences and have been greatly influenced by my experiences there.
This year I am excited to be exhibiting some work in the Bridges Mathematical Art Gallery. You can see my pieces here, and browse the full galleries here. I will also be presenting a short paper on some ideas about teaching mathematics through image manipulation, which relates to my pieces in the exhibition.
Bridges 2013 will be five days of inspiring people, conversations, mathematics, and art! And after that, I’ll enjoy unpacking everything I experience throughout the school year.
Related Posts