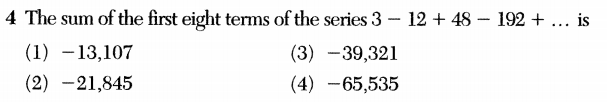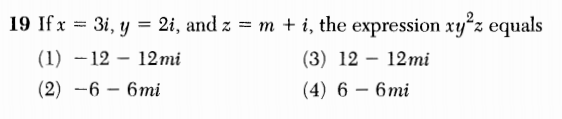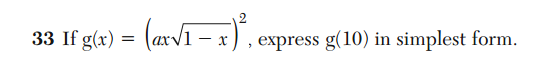MrHonner

Photography

Math Photo: Coordinatization

In order to better understand a space we often impose a coordinate system on it. This allows us to study the characteristics of that space in particularly mathematical ways, like through distance, area, and curvature.

Looking at the city through this rectangular mesh put me in mind of this process of coordinatization, and highlights how the coordinate system is indeed an abstraction from reality and an active choice we make.

By MrHonner, 12 years11 years ago

Challenge NYT

Math Quiz — NYT Learning Network

Through Math for America, I am part of an ongoing collaboration with the New York Times Learning Network. My latest contribution, a Test Yourself quiz-question, can be found here

Test Yourself Math — July 31, 2013

Eike Batista, a Brazilian businessman, has seen his personal fortune drop from $34.5 billion to $4.8 billion in the past year. Approximately how many average Brazilian households is his current fortune equivalent to?

By MrHonner, 12 years7 years ago

Appreciation Teaching

Presenting at MOVES Conference

I am very excited to be a part of the inaugural MOVES conference at the Museum of Mathematics in New York City!

The focus of the conference is the Mathematics of Various Entertaining Subjects, and it features an amazing lineup. Erik Demaine, Dave Richeson, and Henry Segerman are among invited speakers, and Tim Chartier and Colm Mulcahy will be part of special evening of mathematical entertainment!

I will be running a Family Track activity at the Museum on Monday afternoon. This workshop, Sphere Dressing, is inspired by the activity I submitted for the 2012 Rosenthal Prize.

The conference runs August 4-6. You can find out more information here, and see the entire conference program here.

By MrHonner, 12 years12 years ago

Teaching

Regents Recap — June 2013: Encouraging Bad Habits

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Some of the worst exam questions aren’t merely erroneous, but actually encourage students to exercise bad mathematical habits. Consider these questions from the June 2013 Algebra 2 / Trig exam.

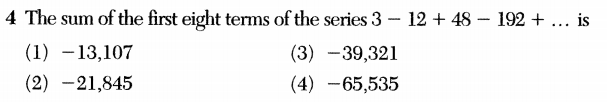
Notice that the problem doesn’t specify what kind of series this is: the student is expected to assume that the series is geometric. This is a terrible habit to encourage, and I wrote about this the last time it happened on a Regents exam. I guess no one is listening.

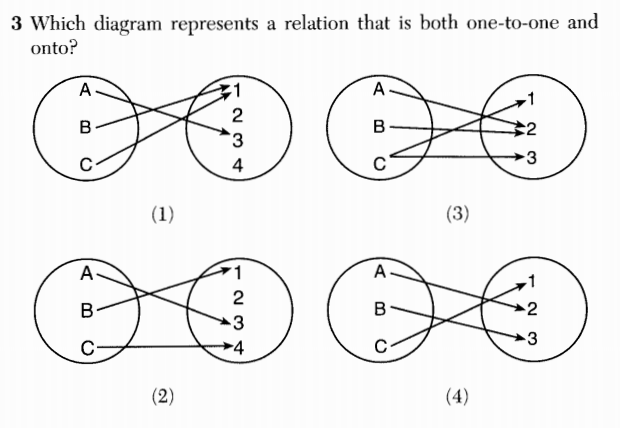
In order to determine whether a relation is one-to-one or onto, it is necessary to know the relation’s domain and range. Here, the student is expected to assume that the oval on the left represents the domain of the relation and the oval on the right represents the range. Perhaps these assumptions are reasonable given the nature of the diagrams, but this just seems sloppy to me. I wouldn’t accept imprecise formulations of functions and relations like this from my students; I would demand they be more explicit. (It’s also worth noting that the relation in (2) is one-to-one and onto its image in the right-hand oval.)

Here’s another example of sloppiness in question construction.

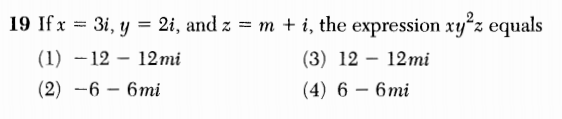
Is it supposed to be obvious that the i here is the imaginary unit? The letter i could be just a variable, like, say, the m that also appears in the question. The available answers support the assumption that 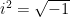$i^2 = \sqrt{-1}$ , but why are we forcing students to play test-detective?

The Regents exams also continue with their long-standing tradition of presenting unscaled graphs, another bad mathematical habit to encourage.

I believe these tests should stand as exemplars of proper mathematics. Maybe I’m alone in thinking this, but it seems to me that repeated exposure to these sloppy exam questions might actually interfere with a student’s ability to truly understand the underlying mathematics.

By MrHonner, 12 years12 years ago

Teaching Testing

Regents Recap — June 2013: More Trouble with Functions

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Functions seem to be an especially challenging topic for the writers of the New York State math Regents exams. After this debacle with functions and their inverses, we might expect closer attention to detail when it comes to functions and their domains and ranges. We don’t seem to be getting it.

Consider this question from the June 2013 Algebra 2 / Trig exam.

According to the rubric, the correct answer is $-900a^2$ . This indicates that the test-makers either (a) don’t understand the concept of domain or (b) they have decided to start working in the world of complex-valued functions without telling the rest of us.

Let $f(x) = ax \sqrt{1-x}$ and $h(x) = x^2$ , and note that $g(x) = h(f(x))$ . In order to evaluate $g(10)$ , we first have to evaluate $f(10)$ . But $f(10) = 10a\sqrt{1-10} = 10a\sqrt{-9}$ , which isn’t a real number. Thus $f(10)$ is undefined; in other words, 10 is not in the domain of $f(x)$ .

But if 10 is not in the domain of $f(x)$ , it can’t be in the domain of $g(x) = h(f(x))$ either. Therefore, $g(10)$ is undefined; it is not $-900a^2$ , as indicated in the rubric.

Of course, if we are working in the world of complex numbers, $\sqrt{-9} = 3i$ . But we never talk about complex-valued functions in Algebra 2 / Trig. When we talk about functions like $g(x)$ , we are always talking about real-valued functions. And just because the process of squaring later on down the line eliminates the imaginary part, that doesn’t fix the inherent domain problem. After all, what is the domain of $f(x) = ({ \sqrt x})^2$ ?

What are the test-makers thinking here? I really don’t know.

Related Posts

By MrHonner, 12 years9 years ago

MrHonner

Follow Mr Honner