A colleague and I had an interesting conversation about a quiz question of his. He asked students to put the four following quantities in order from least to greatest:
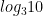
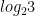


I don’t think I’ve ever written a problem like this for a test or quiz myself, which may explain why thinking about how to assess potential answers perplexed me so. How, exactly, would you grade this problem?
Suppose the correct order is A > B > C > D. A first attempt to grade this problem might be “One point for every item in the correct absolute position”. So
A > B > D > C
would earn two out of four points, as only A and B are in the correct absolute position, while
B > D > C > A
would earn one point, as only the C is in correct absolute position.
But there are some issues with this approach. This response:
B > C > D > A
earns zero points, since no item is in the correct absolute position. But in some sense this response is mostly correct: three of the items (B, C, and D) are correctly ordered relative to each other. Notice also that, in this scoring system, it is impossible to get 3 our of 4 points: the only possible scores are 0, 1, 2, or 4.
My suggestion was to consider all 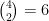 possible pairs of items and award one point for each of the relationships that the response implies is true. For example the arrangement
possible pairs of items and award one point for each of the relationships that the response implies is true. For example the arrangement
B > C > D > A
implies the following correct relationships: B > C, B > D, and C > D. The other three implied relationships are incorrect, thus this response would earn 3 out of 6 points.
The problem with this scoring system is that it is nearly impossible to get a zero! The only response that earns zero points under this scheme is
D > C > B > A
but this answer is compelling in its own way. The correct order is perfectly reversed, which strongly suggests the student knew something about the order of the items.
I like this problem, but I don’t think I”d put it on a test. It’s too hard to assess! But it was fun and mathematically interesting to think about, so maybe I’ll put the question “How would you grade this question?” on a test.
 Through Math for America, I am part of an ongoing collaboration with the New York Times Learning Network. My latest contribution, a Test Yourself quiz-question, can be found here
Through Math for America, I am part of an ongoing collaboration with the New York Times Learning Network. My latest contribution, a Test Yourself quiz-question, can be found here
