Alexander Bogomolny (@CutTheKnotMath) recently posted an interesting interactive diagram entitled “Simultaneous Diameters in Concurrent Circles“. The diagram demonstrates that if three circles intersect in a single point and any two centers are collinear with common chords, then the third center must also be collinear with a common chord.
Inspired by this demonstration, I offer a proof of this fact from a different perspective.
Claim: If two circles centered at A and B intersect at X and Y, and AY intersects circle B at M and BY intersects circle A at N, then the center of the unique circle that passes through M, N, and Y lies on the line through XY.
Proof
We start with the following diagram.

Since NY is a chord of circle A, we know A lies on the perpendicular bisector of NY. The same argument goes for B and chord MY. Construct the perpendicular bisectors and call their point of intersection C. (Note that as long as X and Y are distinct, these perpendicular bisectors can not be parallel).

Notice immediately that C is the circumcenter of triangle NYM, as it is the intersection of the perpendicular bisectors of NY and MY. Thus, C is the center of the circle that passes through N, Y, and M.
Notice also that AM is perpendicular to BC and BN is perpendicular to AC; thus Y is the orthocenter of triangle ABC! (The orthocenter is the point of concurrency of the altitudes of a triangle). Therefore Y lies on the altitude to AB that passes through C. That is to say, CY is perpendicular to AB. But XY is also perpendicular to AB (common chords are perpendicular to lines through centers), so X, Y, and C must be collinear.

Therefore, C is both the center of the circle through N, Y, and M, and C lies on line XY.
Thanks to @CutTheKnotMath for the inspiration! It’s fun to see the orthocenter make an appearance here, as this point of concurrency seems to have fewer applications than its more famous relatives centroid, circumcenter, and incenter. An even more exciting role is played by the orthocenter in this problem.
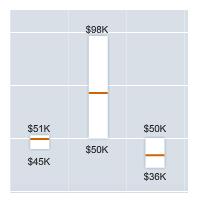 This is a nice chart from the Chronicle of Higher Education that compares average salaries by college major.
This is a nice chart from the Chronicle of Higher Education that compares average salaries by college major.




