Hannah and Her Sweets
Much has been written and tweeted about this problem from a recent math exam administered in the UK:
After the exam, students took to social media to express their outrage at the absurdity of this question. This prompted some reaction pieces from mathematicians and math teachers defending this problem as a demonstration of a link between probability and algebra and as a non-routine problem-solving challenge.
The mathematical status of this problem is less interesting to me than its status as a test item. And as a test item, I think this is not only terrible, but also damaging.
The first eight sentences of this test item clearly indicate to the student that this is a probability problem. Then, it abruptly ceases to be a probability problem and becomes a problem about quadratic equations. No meaningful connection is made between the two concepts: the entire probability story simply exists to establish algebraic conditions on the number n. (And even in a world where contrived test questions are commonplace, this silly story stands out.)
For most students, this test question just reinforces the notion that math makes no sense. And I’m sure others come away feeling cheated, or deceived, by the exam-writers. High-stakes exam questions like this damage student attitudes about mathematics and learning, and have broad, long-term consequences that few people seem to think about.
This problem reminds me of the saga of “The Pineapple and the Hare“. A few years ago, a number of questions on an 8th-grade English exam referred to an absurd passage about a talking pineapple. The passage and the questions were published online, and the ensuing public outcry led to those items being nullified on the exam.
Yet test-writers defended the passage and the items as an effective discriminator: only the highest functioning test-takers could weave their way through the absurdity to answer the questions correctly. Thus, it effectively served to identify the highest performers.
Even if that were all true, why should the navigation of nonsense be a focus of our educational program? And what of the students who come away from such tests feeling demoralized and alienated because a probability abruptly became an algebra problem?
Regardless of what people think about this particular question, I’m glad that, more and more, we seem to be asking the question, “Are these tests any good?“.
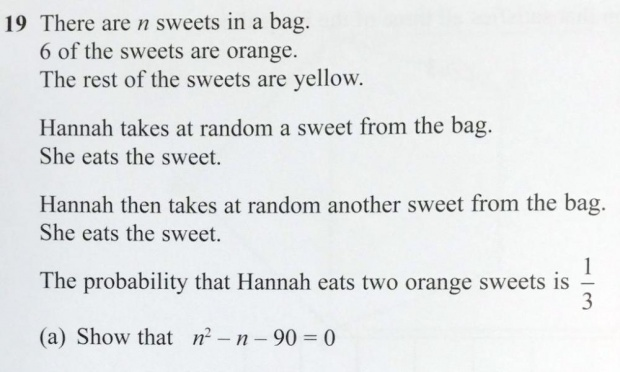
13 Comments
Amy Hogan · June 7, 2015 at 9:32 am
Whuuuuuuuut? Good grief.
Daniel Nissani · June 7, 2015 at 9:07 pm
Can’t agree more with your post! I want to take it further, however, for those who argue that this is a good non-routine problem.
If we look at this as a non-routine problem, then why give such a closed minded way of figuring out n? Instead of finding the number of pieces of candy that would work, you are now given an equation to solve. As you said in your post, no link is made between the probability passage and the quadratic equation given. How great this problem could be if students got the chance to discover that this is a quadratic equation buried under the probability veil!
But to a bigger point, putting a question like this on a high-stakes exam is like putting a question such as find the shortest distance in a prism on the Geometry regents. They are great problems, but at that moment in time, I think they would be best for exploratory activities, not exam questions.
In other words, how non-routine do we want our high-stakes questions to be? And if we want them to be more so, then why not change the pedagogical stance a bit more? Because where we are now, this cannot be the standard. As you said, it will just reinforce students’ poor attitudes towards math. And then we really lost the game.
MrHonner · June 8, 2015 at 3:47 pm
There is definitely an interesting conversation to be had about what these high-stakes exams should attempt to assess. If we want tests to assess non-routine-problem-solving-ability, for example, can such tests be used to fairly evaluate students and teachers in a high-stakes manner? These two ideas seem at odds to me.
Jerome Dancis · June 8, 2015 at 11:51 am
No way is this “a problem about quadratic equations”; no knowledge about quadratic equations is needed or even useful. The student needs to solve a straight forward probability problem, with an unknown, n; this provides an equation in n. Then the students needs to do simple, elementary algebraic calculations to convert the just found equation into the desired equation (which merely happens to be quadratic).
While solving a problem in one branch of mathematics (e.g. probability), it is common that it involves thought or calculations from another branch of mathematics (e.g. Algebra). The exception is textbook mathematics, which keeps the different branches of mathematics in separate silos, thereby hiding many connections between different branches of mathematics. If textbooks regularly included problems, which required the use of two branches of Mathematics (instead of avoiding them), students would become accustomed to them and not freak out when they appear on tests.
Good homework problems should involve teachable moments; but this is not required of one-minute assessment items.
Daniel Nissani · June 8, 2015 at 11:58 am
I would agree with you, except the way the question is asked begs for you to use quadratics. A better way to ask the question is what is n? Or how many pieces of candy in total are in the bag? But asking to show that a related quadratic equals 0 for a certain n makes students think quadratics without connections to the problem.
For us, this is a probability problem through and through. But for kids, who are not as mathematically mature, this is a probability
problem until part (a) and it becomes a quadratics problem.
MrHonner · June 8, 2015 at 3:42 pm
Part (b) of this problem (which is not shown here) asks the student to find n. This requires solving the given quadratic equation.
Of course students should encounter and experience the connectedness of mathematical ideas. But, as much as possible, those connections should be meaningful.
And as a test question, it’s my opinion that this problem and its artificial, irrelevant connection, will do much more harm to student attitudes than good.
Jerome Dancis · June 8, 2015 at 9:29 pm
Are not many of the textbook problems artificial, with irrelevant connections? Do not these many textbook problems collectively do far more harm to student attitudes than an isolated Regents problem? (Your students excepted, since you probably show good taste when assigning homework.)
I’m curious (and a fan of good problems, which make connections), what are a couple of good problems, with realistic connections between probability and simple Algebra that you like?
MrHonner · June 8, 2015 at 10:13 pm
Yes, lots of textbook problems are artificial. And yes, when unchecked, they can erode student attitudes about mathematics. But such problems are part of a ongoing, low-stakes conversation between teacher and student.
High-stakes exams are a very different environment. And structuring the problem in this disjointed way, I think, does a disservice to students who struggle with math.
A great, accessible space where algebra and probability interact is expected value. Evaluating and designing games for “fairness” make for wonderful tasks.
Richard · June 12, 2015 at 3:10 pm
A student can just do the probability question and find n without the quadratic.
Then the only thing element (a) asks is to take that n put it in the quadratic and calculate that the quadratic equates to zero.
If we make maths any more pattern-recognition-like then we may just as well stop teaching because in a few years you just take a photo and Google give you the answer to any pattern-recognition-like exercise.
Hillary Clinton · July 4, 2015 at 7:46 am
This is a ridiculously easy question to answer.
Hannah takes a sweet and the probability it is orange is 6/n. Basic probability.
She takes another sweet. The probability it is orange is 5/(n-1). 5 because she has already eaten one of the 6 orange sweets. (n-1) because she has already eaten one of the n sweets. Simple logic.
The probability she eats two orange sweets is, therefore: (6/n) * (5/(n-1)) Basic probability.
We are then told that the probability of her eating two orange sweets is 1/3, so this gives us an equation: (6/n) * (5/(n-1)) = 1/3
Now, basic algebra says this equates to: 30/(n*(n-1)) = 1/3
multiply both sides by 3 to get: 90/(n*(n-1) = 1
multiply both sides by n*(n-1) to get: 90 = n*(n-1)
and then: 90 = n^2 – n
rearranging gives: n^2 – n – 90 = 0 as required.
This was so trivial that I solved in my head.
Disclosure: Yes, I have a degree in Maths but I am aged 50 and I solved it, so I can only say the people who got angry are not mathematicians.
Trivial.
MrHonner · July 7, 2015 at 3:05 pm
You are mostly right: the people who got angry are not mathematicians. They are math students and teachers who feel that this is a terrible test question. The level of difficultly is not the issue, but the terrible set up.
And for the record, here’s one mathematician who got angry: https://www.waterstones.com/blog/non-fiction-book-of-the-month-jordan-ellenberg-hannah-and-her-sweets.
Hillary Clinton · July 17, 2015 at 6:12 am
Maybe but don’t you think it important to have a few slightly stretching questions? After all, we need to be able to distinguish between the better students and the rest. This outcry smacks of “prizes for all”. I celebrate the exam board for setting this question and hope that it marks the start of the end of grade inflation and trophies for all.
MrHonner · July 17, 2015 at 9:09 am
The “stretching” induced by this question isn’t of mathematics, but of relevance. Questions like this train students to ignore the context of problems, which works against what we are trying to do as educators. See my talk g = 4, and Other Lies the Test Told Me, for a fuller argument.
And this is not about “prizes for all”. It’s about fair evaluation on state-mandated curriculum for all.