Are The New Tests More Rigorous?
The release of student test data from 2013 has educators, administrators, politicians, and parents abuzz in New York. These are the first state exams aligned to the Common Core standards, and as widely predicted, proficiency rates have plummeted, leaving everyone scrambling to explain what has happened.
The most common explanation offered is that these new tests are substantially more rigorous than the old ones, so lower student performance is to be expected. I was curious about the claim that the new tests are more rigorous, and while the state does not release the exams to the public, they do publish a small number of questions from each grade level.
The new tests were administered in grades 3-8. As a high school teacher, I am not well-versed in elementary school tests, but I have spent a substantial amount of time scrutinizing New York state math Regents exams, so I thought I’d look at the 8th grade math questions that were released to the public. I was quite surprised by what I saw.
The “representative sample” of 8th grade math questions does not seem more rigorous to me. They do not seem to emphasize “deep analysis” or “creative problem solving over short answers and memorization”, which is often how the new standards are characterized. I can’t say I was surprised to discover this.
What did surprise me, however, was how many of these 8th grade math questions were virtually identical to questions that have recently appeared on high school math Regents exams.
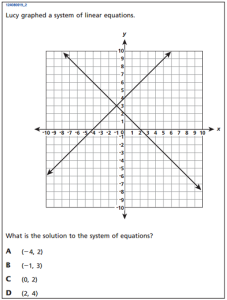
Here is the first example from the set of 8th grade math questions released to the public:
This problem is essentially the same as #4 from the January, 2013 Integrated Algebra exam
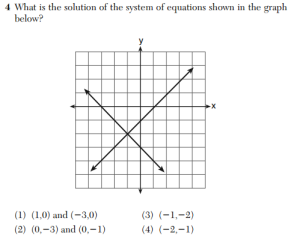
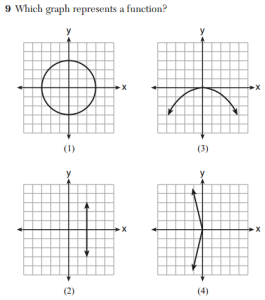
The second example from the set of 8th grade math questions released to the public
is quite similar to #4 from the January, 2013 Geometry exam
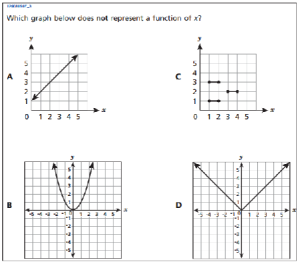
And the fourth example from the set of 8th grade math questions released to the public
is essentially the same as #9 from the January, 2013 Integrated Algebra exam
This surprising discovery left me with a lot of questions.
First, why are 8th graders facing the same kinds of questions on this state exam that 9th, 10th, 11th, and even 12th graders faced this year? Were teachers and students prepared to see this kind of content on the 8th grade exam?
Second, how can it be argued that this new test is more rigorous if it is comprised of the same kinds of questions that appear on the old tests? Simply moving a question from a 10th-grade test to an 8th-grade test doesn’t transform the question into one that requires deep analysis or creative problem solving. More rigorous questions would ask students to construct mathematical objects, explore concepts from different perspectives, and demonstrate mathematical reasoning. None of the above questions do this: they are not especially challenging, deep, or novel. In short, they are typical standardized test fare.
And perhaps the most important question is this: if these are the hand-picked exemplar questions released to the public, what must the rest of the test look like? Only by releasing the entire test to the public can we truly assess what we are assessing.
A version of this post appears at GothamSchools.
12 Comments
Anonymous · August 8, 2013 at 6:05 pm
It’s a real shame that politics plagues our education system in New York City. In addition, we also have rival testing companies that reap in profits through the suffering of students, teachers, and parents. Consider the case when a student receives a Mathematics textbook published by the SAME company that produces standardized exams for the city that the student resides in. Wouldn’t the student have some sort of advantage compared to another student, who could receive a textbook from a different publisher? (Here’s a referenced blog post by a NYS English teacher who makes this case from her current personal experience:
http://dianeravitch.net/2013/04/18/how-pearson-cheats-on-state-tests/
And lastly, I feel that we have the same record playing over and over; students are learning how to take exams, rather than being properly tested for their knowledge/skills in a particular subject.
MrHonner · August 9, 2013 at 9:06 am
The political aspect of public education will always be present. The best we can do, I suppose, is be informed and active in the process.
Amy Hogan · August 9, 2013 at 10:02 am
The nicest thing I can say about these released Common Core test questions is that all the graphs are labeled correctly.
MrHonner · August 9, 2013 at 10:45 am
Good point–perhaps that’s the source of the increased rigor?
Jerome Dancis · August 9, 2013 at 3:54 pm
Rigor or not, knowing which is a function is almost no value to middle school student, even to a Grade 11 student. Poor use of time.
I would prefer to see Grade 8 students use Arithmetic (no Algebra) to solve the Arithmetic problems in
”Supposedly Difficult Arithmetic Word Problems” at
http://www.math.umd.edu/~jnd/Difficult_Word_Problems.html
MrHonner · August 9, 2013 at 4:45 pm
The above uninteresting multiple-choice questions aside, function is a fundamental concept in mathematics. It is also a central idea in much of secondary mathematics (sketching curves in the plane; transformations; trigonometry; calculus). It’s surprising to hear someone argue against its value.
Jerome Dancis · August 9, 2013 at 9:02 pm
Thank you Mr. Honner! You deserve credit for documenting that the sample questions on the first Grade 8 Math state exams supposedly aligned to the Common Core standards are not more rigorous. They do not include “deep analysis” or “creative problem solving”, which is often how the new standards are characterized, by its proponents.
I will forward your blog to interested parties.
As for functions:
It would be useful for fourth graders to be comfortably with using functions (aka formulas), like:
Area of a rectangle is length times width.
In high school, this should morph into A(l,w) = lw.
In Algebra I, students should be comfortably using the formulas for polynomial functions.
Algebra students should be comfortably enough and knowledgeable enough with using polynomials to write formulas (aka functions), which describe and model the situation in an Algebraic Word Problem.
Algebra II, students should be comfortably enough and knowledgeable enough with using polynomials to do this problem:
Find a polynomial function, f(x), such that f(1) = 1, f(2) = 2, f(3) = 3 and f(4) = 4, but f(1) = – Square root 2.
IMHO, not useful to inflict on high school students, the two problems you cited on the NY tests.
For Grade 8, I would much prefer to see students solving Arithmetic word problems, which require analytical reasoning: For example:
Problem 1. As the clock strikes noon, Jogger J is 2500 yards and Walker W is 4000 yards down the road (from here). Jogger J jogs at the constant pace of 10 yard/sec. Walker W walks at the constant pace of 5 yard/sec. How long will it take Jogger J to catch up to Walker B?
Using Algebra, will hide the conceptual understanding of the solution of this problem
Problem 2. “Mrs. Chen made some tarts. She sold 3/5 of them in the morning and 1/4 of the remainder in the afternoon. If she sold 200 more tarts in the morning than in the afternoon, how many tarts did she make?”
Problem 2 is from a 5th grade Singapore math textbook, noted in http://www.cbmsweb.org/NationalSummit/Plenary_Speakers/ma.htm
David Sher · August 11, 2013 at 10:10 pm
Hate word problems that involve solving problems no one cares about. They make math look like a torture we inflict upon students rather than a collection of useful skills. Who cares how many tarts Mrs Chen baked? A more motivated problem can look like this. From 9-12 they charged $1 and sold 200, from 12-3 they charged $.75 and sold 300. Assume a linear demand how much should they charge to sell the remaining 500 before the store closes at 6.
Jerome Dancis · August 12, 2013 at 8:05 am
No students cares about your reworded problem.
No store owner cares about your reworded problem; she/he wants to maximize revenue. He/she would do far better to sell 400 tarts at $.50 EACH than to sell 500 tarts at $.25 EACH.
It is completely unrealistic to assume that the demand is linear.
Fine with me, if you rewrite the tart problem as long as the replacement has equal math content, not one that requires far less conceptual understanding (and also avoids fractions). I hate problems for Grade 8 students, which reflect the low expectations of your problem.
MrHonner · August 12, 2013 at 8:37 am
David and Jerome-
I’d appreciate it if you tone down your comments a bit. You both seem to have constructive things to say, but it looks like this conversation is heading in a negative direction. I’d rather not spend my time refereeing contentious personal disputes here.
Sarah Chauncey · August 14, 2013 at 9:08 am
I thought I’d share a paragraph that my son wrote, at my request in 2009. He is now 23. I think we should ask more students what they think or thought… He is now in an environmental studies program and will be graduating in 2014. He has voiced similar feelings about his college-level chemistry and math courses… I did not change one word — just removed school name.
Teaching Math
Throughout my school years in ______, I can definitely say that every one of
my math teachers was always able to give me a firm understanding of mathematical
concepts. When I went on into high school, I continued to learn and use more and more mathematical processes and techniques. However there were times where we were
learning so many formulas so quickly, that we were never really introduced to how some complicated formulas came about. I know bringing this up might sound pushy when the teachers are trying to get through their curriculum on scheduled time. I also realize that some students (who aren’t that interested in math) may just want to memorize formulas so they can get passing grades. However there will always be students like me who are sort of uncomfortable about not having a clear enough picture of what they are trying to learn and do. I think if the school could find a way to teach the raw mechanics of how mathematical formulas and processes came to be and why they work, then not only would this clarify math to struggling students, but it might also cause more students to take greater interest in class.
Jerome Dancis · January 22, 2014 at 10:41 am
“What does [how students answered the questions on] the International PISA Math Test Really Tell Us?” is the title of my article,” which appeared in American Association of School Administrators Journal of Scholarship and Practice. See Pages 31-42 at
http://www.aasa.org/uploadedFiles/Publications/Journals/AASA_Journal_of_Scholarship_and_Practice/JPS-Winter2014-FINAL.pdf
Answer: Students need instruction in multi-step Arithmetic word problems. Do not rush students into Algebra I in Grade 8.
Difficult Pisa Question “Climbing Mount Fuji”
The Gotemba walking trail up Mount Fuji is about 9 kilometres (km) long. Walkers need to return from the 18 km walk by 8 pm.
Toshi estimates that he can walk up the mountain at 1.5 kilometres per hour on average, and down at twice that speed. These speeds take into account meal breaks and rest times.
Using Toshi’s estimated speeds, what is the latest time he can begin his walk so that he can return by 8 pm?
Internationally, among fifteen-year-old students, one in eight answered this question correctly.
This is basically, a straight-forward four-step problem, albeit one that requires sustained accuracy”.
There are more PISA Math questions at
http://www.oecd.org/pisa/pisaproducts/PISA%202012%20framework%20e-book_final.pdf
The benefit of your perspective will be appreciated.