How Many Sides of a Pentagon Can You See?
Every fall, Math for America celebrates the great work of their math and science teachers with a gala dinner. In addition to food, drinks, and talks from teachers, leaders, and policy makers, the event always features math puzzles to ponder while enjoying the evening’s festivities.
 Here is one of this year’s puzzles:
Here is one of this year’s puzzles:
Suppose you are standing several miles from the Pentagon. What is the probability you can see three sides of the building?
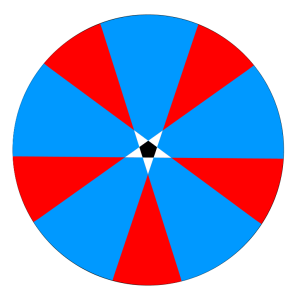
This is a fairly well-known puzzle with a seemingly straight-forward answer. Consider the diagram at right.
The pentagon is shown in black, at the center. Shown in white are the regions where only one side is visible; the regions where only two sides are visible are blue; and the regions where three sides are visible are red.
A simple “solution” is as follows. An infinite red region is essentially equal in area to an infinite blue region, as they differ only by a finite amount: namely, the pentagon itself and three white triangles. So from the perspective of the infinite plane, all finite regions are negligible, and the blue and red areas are equal. Thus, there is a 50% chance you’ll see two sides, and a 50% chance you’ll see three sides.
This is the argument that some colleagues gave, and it is a nice one. However, there’s a slight problem: as stated, the puzzle didn’t suggest that the vantage point was a randomly selected point in the plane. It suggested that the vantage point was a randomly selected point at a fixed distance from the pentagon!
At any finite distance from the pentagon, say D, you are more likely to see two sides than three! As D goes to infinity, the probabilities converge to one-half, but at any finite distance, the blue regions are always slightly larger than the red regions.
To illustrate this point, I created the following animation in Geogebra. At small radii, the blue regions clearly occupy more area than the red regions, but as the radius increases, the respective areas start tend to converge.
So, not only was this a fun puzzle to think about, but it became an object lesson in how important the statement of the problem can be. And in particular, it’s a reminder of how the different ways we model random selection can make for big differences in our solutions!

5 Comments
Andy Rundquist · December 16, 2015 at 2:02 pm
This is a great puzzle. I thought the 50% argument was interesting, as it only works if you really do go out to infinity. I talked with a math prof bud of mine who said you can’t say something like “choose a random point on the infinite plane” because you can’t consider a uniform random distribution on such an infinite plane. Instead he said that you need to consider a distribution that tends to zero as r gets big to have a chance at saying something meaningful. If you do that, then 2 sides wins since you need to go out to infinity for it to get to 50/50.
Dan Anderson · December 16, 2015 at 3:48 pm
You can test the hypothesis out if you come up to Saratoga Springs in the winter when they have this beautiful metal pyramid covering up a fountain. https://twitter.com/dandersod/status/669641801481875456 and https://twitter.com/dandersod/status/669631457862750208
Carl Oliver · January 3, 2016 at 11:07 pm
I remember working on this while we were eating dinner and really racking my brain over the definition of the word “several”. If several were not sufficiently large enough to be approaching infinity, the probability would have to be dependent on the distance from the pentagon. I began working on a function that for a given distance, would give the proportion of total arc length that is red. However it also seems that the infinite case would still be the right one. If several is defined as 10 or so, then the number of miles are far enough that the probability would only be less than 1% different than the infinite case, assuming that my geogebra work made sense.
MrHonner · January 4, 2016 at 8:32 pm
Yes, the uncertainty of several got me thinking that night, too. It’s clear that, if you are really close, you’ll only see one side, which made me immediately skeptical of 50% as an answer.
Getting a formula as a function of d seems messy. But I guess all trigonometry is messy to me.
Noah J. · January 9, 2023 at 7:12 pm
I don’t think the 50% argument works if you go out to infinity, actually. If you draw a line going through the center of the pentagon that’s parallel to one of the sides of the pentagon and stand on either end of that line, you’ll always see two sides. This means you’ll always have a slightly higher chance to see two sides.
I mean, that infinitesimally small chance might be treated as nothing, so I might be wrong. Plus, even if you go out that far, you can’t be viewing from a singular point, since you have two eyes, but that might just mean you’ll be seeing *three* sides more often, instead.