Regents Recap — June 2015: Common Core Geometry and Transformations
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
June, 2015, saw the administration of the first Common Core Geometry Regents exam in New York. I led a teacher team that worked to adapt our curriculum to the Common Core standards. One of our primary concerns was how the new transformation-based approach to Geometry inherent in the Common Core standards would be represented on this Regents exam. In particular, we had no idea how establishing congruence and similarity via transformations, an apparent emphasis of the standards, would be assessed.
A total of 18 of the 86 points on the exam (around 21%) were associated with transformations: six multiple choice questions and two free response questions. Here are a few examples, with associated Common Core standards in parentheses.
Question 10 is about rotations that map regular polygons onto themselves (CCSS.MATH.CONTENT.HSG.CO.A.3).
Question 16 assesses the concept that dilation can alter length but must preserve angle measure (CCSS.MATH.CONTENT.HSG.SRT.B.5).
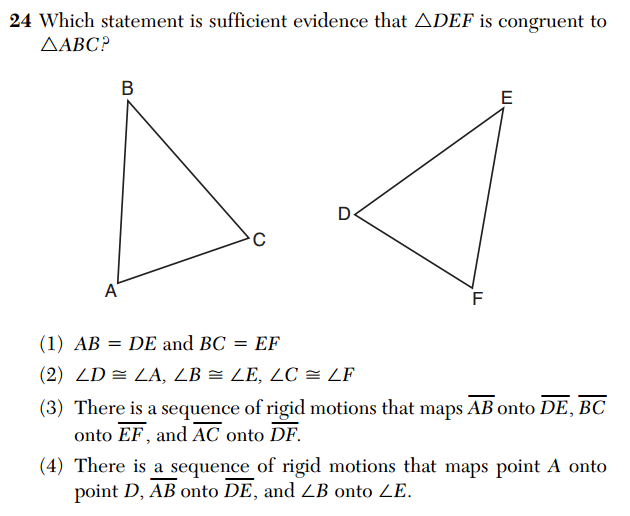
Question 24 addresses establishing congruence by rigid motions (CCSS.MATH.CONTENT.HSG.CO.B.7).
Question 30 asks the student to explicitly connect transformations to congruence by recalling the fundamental principles that underlie rigid motions (CCSS.MATH.CONTENT.HSG.CO.B.6).
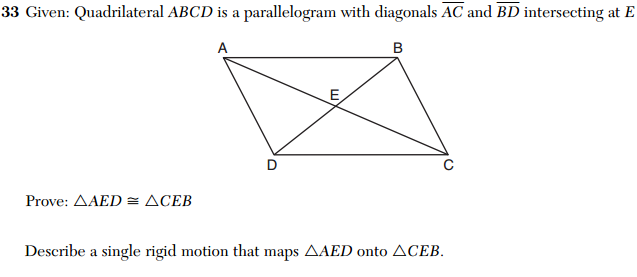
And Question 33 asks to student to first produce a “traditional” proof of congruence, and then interpret the congruence through a rigid motion (CCSS.MATH.CONTENT.HSG.CO.C.11). This is a simple way to connect the two concepts.
Overall, the manner in which transformations were tested aligned with our expectations, both in scope and in content. Our Geometry worked closely together throughout the year, integrating a variety of resources from New York state and elsewhere, but mostly felt in the dark about what the test would look like. In the end, we were pleasantly surprised. But we also noticed how much different the Common Core Algebra exam was in year two, so we know that we may be surprised again.

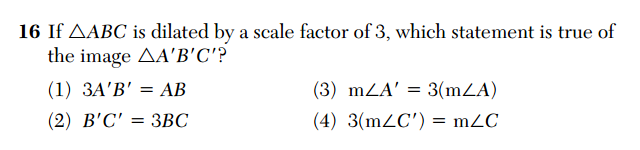
0 Comments