Derivatives of Vector Functions

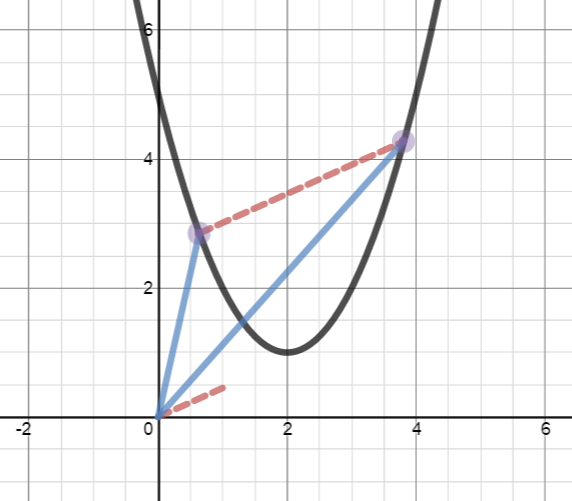One way to think of a curve in the plane (or in space) is as a collection of terminal points of vectors whose initial points are all at the origin.  The vectors are given by a vector-valued function.

For example, the parabola shown at right can be thought of as the graph of the vector-valued function

I’ve created a Desmos demonstration that shows how graphs of vector-valued functions are related to their vectors (shown in blue), and how the derivative of a vector-valued function is related to both difference vectors and tangent vectors.  You can access the demonstration here.

You can find more of my Desmos demonstrations here.