Regents Recap — June 2014: What is an “Absolute Value Equation”?

Published by MrHonner on July 28, 2014July 28, 2014

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The following question appeared on the 2014 Integrated Algebra exam.

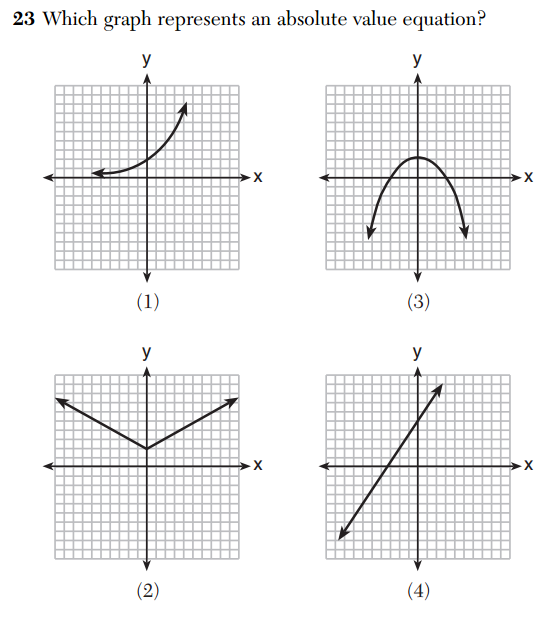My question is this: what, exactly, is an “absolute value equation”? According to the scoring key, the correct answer to this question is (2). This suggests that the exam writers believe an “absolute value equation” to be some transformation of $y = |x|$ .

But “absolute value equation” is not a precise description of what the exam writers seem to be looking for. It would be hard to argue that $y = |2b^{x}|$ is not an “absolute value equation”, but that appears to be the graph depicted in (1). With some work, all the given graphs could be represented as equations involving absolute values (an exercise left to the reader).

I doubt this imprecision caused any student to get this question wrong, but as I have argued again and again, these exams should stand as exemplars of mathematical precision. These exams should not model imprecise language, poor notation, and improper terminology. We do our students a great disservice by constantly asking them to guess what the exam writers were trying to say.

4 Comments

CCSSIMath · July 28, 2014 at 4:42 pm

Yep, creating such ambiguity is a bind that exam authors often put themselves in when attempting to distill mathematical concepts into multiple choice questions that test tiny “math bites”.

It is also a sad commentary that students’ ability to understand and proceed on such questions should hinge on issues of “language”, “notation” and “terminology”. NYS Regents have for decades been the most anally-retentive exams, penalising students for failing to distinguish between “congruent” and “equal”, as an example.

At the other end of the spectrum are complete soup-to-nuts problems that gauge not only students’ understanding of a concept, in this case, absolute value, but the ability to apply the concept to problem solving.

Here’s one example: http://bit.ly/1tTN6kP

We realise that the kind of problem that takes 10-15 minutes or more of uninterrupted work to completely solve is not likely to make its way into Regents exams or American Common Core exams of the foreseeable future, but it lays bare the chasm: such lengthy (and unambiguous) questions are standard fare in top-performing mathematics nations.

Geoff · July 30, 2014 at 9:00 am

That’s a great catch, Patrick. It could also be (4), assuming the critical point of the function isn’t within the frame of view. Something like,

y=|(3x+25)|-20

This speaks to test-writers presuming that students will know what their intent is. It’s like, “a student that’s done well knows what we *really* mean”.

MrHonner · July 30, 2014 at 9:40 am

That’s an excellent point, Geoff; I hadn’t even thought about the possibility of (4) being a transformation of y=|x| with its vertex out-of-frame.

As someone on G+ demonstrated, it can actually be a line and an absolute value equation. https://plus.google.com/u/0/+PatrickHonner/posts/7P3JTPCeskR

pasmith · August 1, 2014 at 2:01 pm

Any function whose graph is symmetric about the y-axis is even, and so a function of |x|. (2) and (3) are both special cases of this.

In view of the given answer, I think one must regard the actual question as being “Which of these graphs was obtained by taking a *non-even* function f(x) and graphing f(|x|)?”