When Desmos Fails
I am huge fan of Desmos, the free online graphing calculator. I use it almost every day in my classroom: to sketch simple graphs, demonstrate mathematical relationships, and dynamically explore mathematical situations. And like most worthy instructional technologies, it’s really a learning technology: it’s easily accessible to students as well as teachers..
As far as technology goes, Desmos works very well. But some of my favorite mathematical questions arise when technology does something we don’t expect.
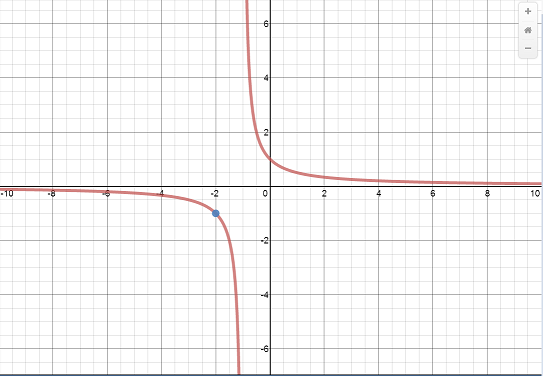
For example, here’s the graph of . This graph has a hole (a removable discontinuity) at the point (-2,-1), which I have colored blue.
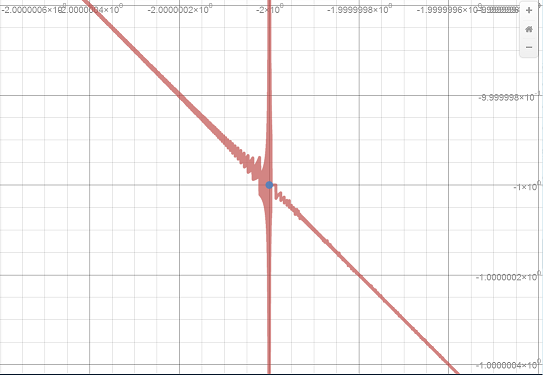
But look what happens when you zoom in around the hole:
At a very small scale, some very curious behavior emerges!
Now, it’s not the function here that’s behaving strangely: its behavior is well-understood. It’s the mathematical technology that is behaving strangely, as it tries to represent the function.
Lots of interesting questions emerge from such anomalies, and these are great questions for students to explore. In doing so, they’ll not only learn some mathematics and some computer science, but they’ll also develop a healthier relationship with technology, by learning to understand how it does what it does, and perhaps more importantly, what it doesn’t do. I explore this theme in greater depth in my talk “When Technology Fails“.
You can find more of my work with Desmos here.
Related Posts
36 Comments
Sue VanHattum · November 21, 2013 at 9:36 am
I hope I’m not being too dense… What questions emerge, and how would one (student or otherwise) go about exploring them?
I remember telling students that the TI did asymptotes wrong because it connected the dots. Desmos is clearly more sophisticated, and I draw a blank when I try to imagine what would cause that strange behavior.
Sue VanHattum · November 21, 2013 at 9:45 am
I thought you were saying that Desmos colored the dot blue. But when I enter this equation, Desmos doesn’t show the hole.I get lots of different odd behaviors as I zoom in. Now I’m eager to find out more about what’s happening. I know the problem is dividing by a number that’s so small the limits of the calculator interfere with accuracy. But it’s weird the shape that takes.
MrHonner · November 21, 2013 at 1:25 pm
Sue-
Sorry I confused you with the blue dot–I colored that in, myself (and changed the language to make that clearer).
The immediate queston that arises for me is “What procedure is this technology employing to graph this function?” Is it just plotting points? Is it using some kind of differential approach? This could lead into a nice project researching these different techniques.
On the purer computing side of the problem, I’m curious about how small numbers are represented in this programming environment, and what effect that has on this rendering. This could also lead to some interesting work.
Cameron Fitzpatrick · June 14, 2016 at 10:27 pm
I’m pretty sure the small and big numbers are represented by what is known as strings in a vector (a list that grows in size as needed)
and what may be happening here is it is running out of memory and you are getting garbage values for your output – for instance when you define a variable in a system it allocates memory for it – however once you go out of the bounds and run out of room on the stack, your system will start doing odd things and displaying what is known as “garbage values”
I should note that when you define a variable and allocate the space – it erases the value that is already there (the garbage value) deleting it and resetting it to the new value you set
these usually contain weird character, huge hex numbers, or addresses.
some how when you zoom in that low you are accessing garbage values in a container.
Elizabeth Greene · May 31, 2018 at 12:29 pm
Desmos will show the hole if you move the cursor to where you think it should be and left click and hold. 5/31/2018
Evelyn Lamb · November 21, 2013 at 7:15 pm
Interesting! Did you actually use this example in class? I’m curious how the students would approach this.
MrHonner · November 21, 2013 at 8:16 pm
We discovered it in class. We were looking at the rational function, and students complained that they couldn’t see the hole. I responded “Well, it’s probably because we just haven’t zoomed in enough!”.
We were all pretty surprised at what we found!
Sid · May 11, 2020 at 9:06 am
Wow… That is a nice moment to feel
Alan Eliasen · November 22, 2013 at 3:42 am
This looks like it’s quite probably an artifact of using “interval arithmetic” techniques to graph the equations. Interval arithmetic is a relatively new branch of mathematics that represents each number as an interval within a certain range, say, [1,3], but you’re not sure where the true value may lie within that range. As intervals are added or multiplied with each other, those uncertainties are propagated through all your calculations.
Interval arithmetic is almost magically powerful when it comes to graphing arbitrary equations. (Try to teach a computer how to graph an equation that contains arbitrary expressions of x and y using any other technique.) However, it can be done in only a few lines of code using interval arithmetic techniques. For example, here’s an intentionally simple example of a program written in my programming language Frink ( http://futureboy.us/frinkdocs/ ) that can plot arbitrary equations using interval arithmetic techniques, *in only a few lines of code!*
http://tinyurl.com/kfw5dxf
(Be sure to follow the “view the source” link to see how ridiculously simple this program actually is, yet it can easily plot equations that you or I couldn’t begin to guess the behavior of!)
The appearance of the graph that you posted looks exactly what happens when using interval arithmetic techniques around a singularity, though. Especially if it’s losing precision badly. The bands start to widen, indicating growing uncertainties, near points where division by zero starts to occur.
Frink does interval arithmetic natively, allowing you to play around with this very powerful technique very easily, but the simple examples I’ve posted don’t try any detailed tricks to refine errors around singularities.
There’s more about how naive interval arithmetic graphing looks around a typical singularity here:
http://www.peda.com/grafeq/tutorials/win/HowGrafEqWorks.html
Check out that program, GrafEQ. It’s really cool. It is smarter than most interval arithmetic graphing programs, as it has knowledge of the continuity of mathematical expressions, which allows you to refine your knowledge of the behavior of a function where it begins to behave badly.
For everything you want to know about using interval arithmetic techniques for graphing equations, absolutely read the author of GrafEQ, Jeff Tupper’s, thesis on the subject:
http://www.dgp.utoronto.ca/people/mooncake/msc.html
Also, the GrafEQ “Gallery” “Rogue’s Gallery” pages are very interesting. Try plugging some of those expression into other graphing programs and see how badly they explode.
Alan Eliasen · November 22, 2013 at 4:08 am
By the way, I posted a higher-resolution version of how a naive interval arithmetic graphing implementation plots that graph here:
http://futureboy.us/temp/honner.png
It was plotted by one of these very simple Frink programs. (Try to write an arbitrary equation-grapher with less code!)
You can see that the behavior around singularities behaves similarly: bands are broadened until they smear out around the asymptote, etc. The program plots in red where we are dividing by an interval containing zero (there are actually ways to meaningfully divide by zero in interval arithmetic!)
http://futureboy.us/fsp/colorize.fsp?f=simplegraph2.frink
http://futureboy.us/fsp/colorize.fsp?f=simplegraph3.frink
(The second link is a slightly more complicated but faster recursive version.)
Here’s how the simplified algorithm works, in a nutshell:
1.) Break the plane into little rectangles.
2.) For each rectangle, treat the x and y bounds of that rectangle as a little interval. For example, if the x bounds of the little rectangle you’re looking at is [0, 0.1], assign that interval to x:
x = new interval[0, 0.1]
and do the same sort of thing for the y bounds of that rectangle.
3.) Plug those values of x and y into the equation you’re graphing. Change the “=” operator in the equation to “PEQ” (the possibly-equals operator in Frink.) PEQ returns true if the two sides of the equation are *possibly* equal, that is, if there’s some overlap between the interval solutions of the right- and left-hand side of the equation within those intervals.
4.) If those numbers are possibly equal, (i.e. PEQ returns true,) plot the point.
Incredibly simple, but incredibly powerful. Again, I don’t know if this is how Desmos works, but it behaves similarly enough that I’d certainly wager that it uses interval arithmetic techniques.
MrHonner · November 22, 2013 at 7:32 am
Alan-
Thanks for this clear and insightful introduction to interval arithmetic, something I’d considered but never knew actually had been implemented. It makes a lot of sense; essentially it’s a probabalistic approach to graphing, which I suppose when you think about it, is probably exactly how an approximation device should go about plotting a graph.
I’m curious to learn more about GrafEQ, a program I’ve played around with. In particular, I’m fascinated by how it could have “knowledge” of continuity.
You’ve given me a lot to think about here–thanks for that! And for the nice graph!
PH
Alan Eliasen · November 22, 2013 at 6:47 pm
One of the cool, almost magical things about interval graphing techniques is that they are one of the only techniques that *aren’t* probabilistic if implemented correctly. Unlike other probabilistic sampling techniques for graphing equations, they can’t “miss” a solution (like a sharp vertical asymptote) by not sampling enough and getting unlucky.
For example, the “spike” example in the GrafEQ “Rogue’s Gallery”:
http://www.peda.com/grafeq/gallery/rogue/spike.html
I have an example of that graph plotted by Mathematica which misses the vertical spike entirely and plots the graph as a smoothly increasing straight line. An interval plotting algorithm could not miss that spike.
As you could see in my samples, simple interval algorithms may tend to “overestimate” their boundaries, making them possibly incorrectly state that there *may be* a solution in a given interval, (you see this with broadening lines) but this problem can be solved by sampling more, smaller intervals, or by using continuity information.
The great thing about even the simplest interval algorithm is that it will never “miss” solutions by not sampling finely enough. (This also makes interval arithmetic great for optimization problems; they won’t accidentally miss a global or local optimum. That’s *extremely* powerful.)
GrafEQ claims to be “pixel-perfect” in its graphs when possible. If a solution exists within that pixel, that pixel is plotted, otherwise it isn’t.
Establishing continuity is a difficult problem that requires that all mathematical operators in your programming language can be queried to determine if they’re continuous over a given range of arguments. I’m part of a couple expert groups that are attempting to define interval arithmetic standards for IEEE and the C++ language, among others. We’ve been slowly working toward consensus on a standard way to indicate continuity. What we’re converging to is a small number of flags (around 5 states) that will be carried along with each interval as it is calculated, indicating, say, that the interval was known to be defined and continuous over the range it was calculated, or if the interval was somewhere undefined or discontinuous in the range it was evaluated, or if it was nowhere defined.
This knowledge of continuity is not available in most existing calculating environments, so all mathematical operations in the language must be extended to support it, beyond the work you have to perform to do basic interval arithmetic in the first place.
Interval arithmetic is surprisingly powerful in many areas, and well worth further study!
MrHonner · November 23, 2013 at 7:22 am
By ‘probabalistic’, I wasn’t thinking ‘sampling’: I was thinking more of the switch from a binary truth-value (0 = False, 1 = True) to a continuous one, where truth is expressed as an interval. Thus the equality of two values is measured by the overlap of those intervals, although it sounds like in your programming language, the magnitude of this intersection isn’t relevant.
This really is interesting stuff–the kind of computer science that actually appeals to an abstract-minded mathematician! Thanks so much for providing such a thoughtful overview here–I know I’m not the only the one who finds it fascinating.
Looking forward to learning more!
Alan Eliasen · November 4, 2014 at 6:52 pm
By the way, here’s Mathematica failing drastically in graphing the graph I mentioned above. It uses the Twitter account @wolframtap which evaluates a Mathematica expression and displays the result:
https://twitter.com/aeliasen/status/512798798641233921
Obviously, the equation ( y = (x^2 – 3x) / (x – 3.0001) ) should go to positive and negative infinity around x=3, so you can see even very expensive mathematical products fail badly in ways that the simplest interval arithmetic solution can’t fail.
Earl · November 23, 2013 at 9:59 am
Different focus: This is a great opportunity for students to evaluate second derivative over the intervals in question to verify that the technology is incorrect.
Patrick Reynolds · November 23, 2013 at 3:23 pm
(Long-time listener, first-time caller here)
Thanks for introducing me to Desmos; I had been thinking of using Geogebra extensively when I teach calc next term, but am now thinking of using Desmos. Apart from interface considerations, I wonder what the technological/computational issues are that I should consider.
Also, I’m curious what the mood in the room was like when you discovered the zany behaviour. Exasperation with technology? Or do you suppose it helped anyone digest why dividing by zero or “almost zero” should be treated with care?
MrHonner · November 23, 2013 at 6:14 pm
Hi Patrick-
Thanks for chiming in (and for listening!).
As I said, I pretty much use Desmos everyday in calculus. Geogebra is definitely a more robust environment, but Desmos is much easier and more intuitive to use. It doesn’t do any of the relationsl geometry that Geogebra does, but in terms of quickly and beautifully sketching interactive graphs, it’s invaluable.
We didn’t spend much time talking about it in class–I was quite surprised, and we quickly chatted about what we thought might be the reasons behind it. No exasperation, though–we had to work pretty hard to find the glitch. And I hope the students have learned to understand the limits of technology.
DD · May 23, 2014 at 9:56 am
Isn’t this just floating point precision issues? As you approach the hole, floating point precision becomes insufficient to properly calculate the result because the calculations are made with, effectively, a limited number of decimal places, too few for the ratio being calculated. The result is numerical errors as you approach the hole.
DD · May 23, 2014 at 10:13 am
Here is a demonstration of the floating point inaccuracy. Basically, there is insufficient precision close to the hole as you can see (the dot is moving according to a very small change in x around the hole). https://www.desmos.com/calculator/uews9uyi0z
Scott · July 3, 2014 at 12:50 am
Came across this same issue this year myself. Thank you for chasing this down and once again you expand my mathematical knowledge.
Scott
ihor charischak · December 23, 2014 at 6:32 pm
I apologize if this is a knaive question since I haven’t looked at a rational function since I was studying calculus in college… but wouldn’t it make sense to reduce the rational function to 1/x+1 and make this easier to analyze?
MrHonner · December 23, 2014 at 7:33 pm
The issue is that (x+2)/(x^2 + 3x + 2) is undefined at x = -2, thus there is removable discontinuity at (-2,-1). This “hole” in the graph is the source of the graphing failure. Note that 1/(x+1) is defined at x = -2, so there is no discontinuity at x = -2 for that function.
ihor charischak · December 24, 2014 at 6:38 pm
I understand that. What I was intrigued about was that “reducing” the original form of the function does not yield an equivalent function. My intuition suggests that they should be equivalent.
Bob Jones · May 1, 2015 at 7:20 pm
Hello, Mr. Honner. If Desmos did what it was supposed to do, it wouldn’t have even shown it. No matter how much you zoom in, it is an exact point where this doesn’t work and shouldn’t even be able to be seen. Just think about it. However, I do find the behavior to be a bit strange. How does the program make that when it finds out a value does not compute? How does it handle this error?
Nahil Sobh · November 13, 2015 at 9:51 am
If one factors the denominator to (x+1)(x+2) this behavior disappears 🙂
Sky · December 10, 2015 at 2:04 pm
Found something that seems interesting: https://www.desmos.com/calculator/vzltqmzu5u from my knowledge this is supposed to graph sinx but at 44 and above it starts acting funny.
Marangeli · January 30, 2016 at 5:50 am
I tried this rational function: f(x) = (x^2+4x+4)/(x^2-4). I understand that if a factor in the denominator is also in the numerator an equal amount of times, there will be a hole at that zero. I also understand that if the factor in the denominator is also in the numerator, but more times in the numerator (greater multiplicity), there will also be a hole at that zero. Turns out this function (when using Desmos) will show an x intercept at x = -2 instead of a hole. Other functions with holes, when graphed with Desmos, will show me the coordinate of the hole as example: (5, undefined). For the function mentioned above, it shows the coordinate (-2, 0) as an intercept and actually crosses the x axis. I do the sign analysis before I graph and this intercept is not considered because it’s a hole. I have told my students that we only consider x intercepts and vertical asymptotes for the sign analysis. Should I consider this as an intercept in the sign analysis even though it’s a hole? Thank you for any input you may have.
MrHonner · January 31, 2016 at 8:20 pm
I’m not sure exactly what you mean by “sign analysis” here, but continuity is usually at the heart of all sign / interval analysis.
Since x = -2 isn’t in the domain of the function, the function can’t be continuous across x = -2. This means the function could be behaving very differently on either side of x = -2. So you definitely have to consider it in your analysis, even though it’s not an intercept.
LjSpike · March 6, 2017 at 10:13 am
Just an observation, clicking on -2 yields (-2,undefined) so desmos hasn’t failed in its calculation, just plotting, which I wouldn’t blame it for, after all, how do you show undefined? 😛
The exact reason I suspect is that at the scale you’ve zoomed in desmos performs some interpolation to display the image, as the shear number of decimal places involved is so great it’d eat too much memory to actually calculate, but as it gets even further zoomed in, it has no points on the screen to interpolate, but it must show something as those points aren’t exactly the value of x=-2 so must be defined, and the equation then “falls over” as my computer science textbook would’ve said.
Shazyam · June 29, 2018 at 5:15 am
When you do factorial it screws up especially when its like 3x factorial
Brandon · October 26, 2018 at 4:35 pm
x^(1/3) is interesting: it graphs points that are negative (you can’t do that).
1/3 as an exponent is the same as 0.6 (with the 6 repeating). Doing x^0.666666 does show the right graph.
Which makes me wonder how Desmos deals with exponents.
KC · November 28, 2018 at 4:32 pm
Brandon, two things: #1. Negative values are in the domain of x^(1/3). 🙂 E.g., the cube root of -8 is -2. #2. x^(1/3) is x^0.333… x^0.666… is x^(2/3).
DesmosBreaker · February 8, 2019 at 4:13 pm
got the same thing to happen horizontally on point (-1,-2) with the equation x=\frac{y+2}{y^2+3y+2}
Joey Zahorik · March 8, 2019 at 1:03 pm
You can have the opposite of this happen if you plug in these four equations:
(-|x|+1)+x+y=|y|
(-|x|+1)+x-y=|y|
(-|x|+1)-x-y=|y|
(-|x|+1)-x+y=|y|
Once you do this zoom out to around 2×10^16
You can also have some strange things happen if you plug in a convoluted equation that scribbles on the graph and then start to wonder around the graph you’ll start to see the same rectangular pattern appear on the bottom left of the window regardless of where you are on the graph or how far you are or aren’t zoomed in.
Another thing that seems to trick desmos out is when you have multiple y solutions for one x input
Joey Zahorik · March 8, 2019 at 1:04 pm
*zoom out so you max x and y are 2×10^16 and min x and y are -2×10^16
John Sellers · June 6, 2020 at 4:49 am
I don’t know the specifics, but I am not surprised at this kind of flaw. I tried it, but didn’t see it until I zoomed by a factor of about a million or more.
It is a bit of a nitpick. The zoom is so much that you are noticing is like noticing a single microbe on your dinner plate. Surprise, surprise! Nothing is perfect.
You need to understand that all technology has boundaries, and the more range of depth there is, the more boundaries there are to go around, so is it surprising that sooner or later they manifest themselves? The fact is that there are limits on ALL systems. Otherwise, a cell that is dividing would cover the whole Earth in a few days except it runs out of food….thank goodness.