Regents Recap — June 2013: More Trouble with Functions

Published by MrHonner on July 22, 2013July 22, 2013

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Functions seem to be an especially challenging topic for the writers of the New York State math Regents exams. After this debacle with functions and their inverses, we might expect closer attention to detail when it comes to functions and their domains and ranges. We don’t seem to be getting it.

Consider this question from the June 2013 Algebra 2 / Trig exam.

According to the rubric, the correct answer is $-900a^2$ . This indicates that the test-makers either (a) don’t understand the concept of domain or (b) they have decided to start working in the world of complex-valued functions without telling the rest of us.

Let $f(x) = ax \sqrt{1-x}$ and $h(x) = x^2$ , and note that $g(x) = h(f(x))$ . In order to evaluate $g(10)$ , we first have to evaluate $f(10)$ . But $f(10) = 10a\sqrt{1-10} = 10a\sqrt{-9}$ , which isn’t a real number. Thus $f(10)$ is undefined; in other words, 10 is not in the domain of $f(x)$ .

But if 10 is not in the domain of $f(x)$ , it can’t be in the domain of $g(x) = h(f(x))$ either. Therefore, $g(10)$ is undefined; it is not $-900a^2$ , as indicated in the rubric.

Of course, if we are working in the world of complex numbers, $\sqrt{-9} = 3i$ . But we never talk about complex-valued functions in Algebra 2 / Trig. When we talk about functions like $g(x)$ , we are always talking about real-valued functions. And just because the process of squaring later on down the line eliminates the imaginary part, that doesn’t fix the inherent domain problem. After all, what is the domain of $f(x) = ({ \sqrt x})^2$ ?

What are the test-makers thinking here? I really don’t know.

Related Posts

Categories: TeachingTesting

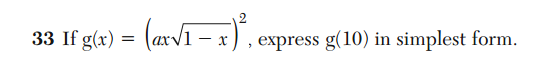
20 Comments

Mike Lawler · July 22, 2013 at 11:35 am

This one is particularly horrifying.

Out of curiosity, I take it from your post that the “correct” answer was published. Was a full solution published, or just the answer? An official full solution to this problem would be pretty illuminating.

MrHonner · July 22, 2013 at 11:46 am

There are never any “official” solutions published. But the sample student responses (http://www.nysedregents.org/a2trig/613/trig62013-srsw.pdf) tell you everything you need to know.

Mike Lawler · July 22, 2013 at 1:58 pm

The sample responses show that they writers were anticipating students manipulating complex numbers.

I clicked around on the nysedregents.org site and found this document:

http://www.p12.nysed.gov/assessment/hsgen/archive/mc-trig-05.pdf

linked on this page:

http://www.p12.nysed.gov/assessment/math/math-hs.html#a2trig

(see “Mathematics Core Curriculum for Algebra 2/Trigonometry”)

The word “complex” appears in three places:

In “Variables and Expression”

A2.A.17 – Simplify complex fractional expressions

In “Number sense and Operations”

A2.N.8 – Determine the conjugate of a complex number

A2.N.9 – Perform arithmetic operations on complex numbers and write the answer in the form a + bi.

Of the three, the last one comes into play in some of the student responses, though this particular problem seems like quite a curious way to test mastery of A2.N.9.

Far more relevant to the question are some of the bullet points in the “Patterns, Relations, and Functions” section:

A2.A.39 – Determine the domain and range of a function from its equation.

A2.A.40 – Write functions in functional notation.

A2.A.41 – Use functional notation to evaluate functions for given values in the domain.

A2.A.42 – Find the composition of functions

There’s certainly no indication at all that students should expect to find questions about complex-valued functions on the Algebra 2 and Trigonometry exam.

If you were trying your best to justify this question, you’d have to appeal to A2.A.41, it seems, and appeal particularly to the phrase “for given values in the domain.” The argument would be that since the test asked the student to evaluate at x = 10, x = 10 must be in the domain. I’d love to see someone try to make this argument with a straight face.

On a more serious note, what I’d really love to know is if a student wrote that x = 10 was not in the domain and thus g(10) was not defined, what score did that student receive?

MrHonner · July 23, 2013 at 7:56 am

As you, yourself, point out, even your best attempt at justification is laughable. I just can’t believe stuff like this makes it through to tests that reach thousands of students.

To answer your last question, the student would most likely receive 0 points based on the rubric.

Mike Lawler · July 23, 2013 at 7:43 pm

This mistake on the exam seemed so horrible to me that I wanted to read as carefully as possible through background material for the exam to see if there’s any possible way to explain how this question appeared on the exam. There’s nothing, and any attempt to try to justify the question based on the curriculum would be beyond absurd (as I was trying to point out above – hopefully it didn’t come across as a serious attempt to justify the question).

What really gets me about this one is that (i) the kids who actually understood the question likely received 0 credit, and (ii) the kids who mostly understood it may have spent quite a bit of time wondering if the answer was “doesn’t exist” or -900a^2. That time could have been put to much better in other parts of the test.

I hope the work you are doing to investigate these questions receives the attention it deserves. It is probably too much to hope that these exams will go away (and, in fact, they’ll more likely spread all over). Hopefully the work you are doing will reduce or eliminate similar errors on future exams.

MrHonner · July 23, 2013 at 9:59 pm

I knew you weren’t attempting a sincere defense of the problem, and I appreciate your honest attempt to truly understand the context by playing devil’s advocate. It helps me refine my understanding, too.

I think about your second point a lot. A student in my class would know the answer is “undefined”, but they would probably also be smart enough to know these exams aren’t smart enough to ask that kind of question. But it’s sad that students have to waste their intellectual energy interpreting these silly exams.

And sad, too, that all teachers in NY are now directly evaluated based on how their students perform on these poorly devised exams. That’s the real reason I keep writing these pieces. With the proliferation of testing to unprecedented levels, no one ever discusses whether these tests are actually any good. I hope the question makes it to conversation some day.

Robert Talbert (@RobertTalbert) · July 23, 2013 at 9:46 am

Actually in my Algebra II class we *did* do complex numbers, but that was in 1986 (shortly after the invention of complex numbers, I think). I have no idea if that topic is touched upon today. Based on what my students seem to know about complex numbers now, I seriously doubt it. So this gets my “facepalm of the day” nomination (although it’s still early).

MrHonner · July 23, 2013 at 9:53 am

Robert-

Complex numbers are in the curriculum, but only real-valued functions are ever discussed in the course.

Matt McIrvin · July 23, 2013 at 10:37 am

What they’re thinking is that the student will do some algebraic manipulations and simplify the function to a^2 x^2 (1-x), then substitute in x=10. In other words, they’re not thinking enough.

MrHonner · July 23, 2013 at 11:25 am

The sample “correct” student work provided by the state suggests even less sophisticated thinking on the part of the writers.

http://www.nysedregents.org/a2trig/613/trig62013-srsw.pdf

Math Skills Coach · July 28, 2013 at 10:44 pm

IMHO, this is an excellent problem to ask students. The truth of the matter is that real mathematics, as practiced everyday by professional mathematicians, often has to break with rules “in neat little boxes”, and just plow through with ‘mindless’ symbol manipulation without regard as to validity of the intermediate steps, only afterwards is justification sought or even warranted. Often the justification is left to lesser mathematicians as the great minds often have little patience for such trivialities. As Einstein said, “Small things amuse small minds.” Much like the quote musicians often repeat, “Wait a minute! Should we tune first? No, Lou Reed wouldn’t tune first! Let’s just play.” Some of the greatest mathematicians of the past, like Euler or Frobenius, paid little heed to ‘correct’ procedures. Ditto for the person that invented imaginary numbers (can’t recall who is credited with that leap of imagination.) By the way, symbol manipulation is rarely ‘mindless’, knowing just what to do next to achieve your goal is one of the most creative aspects of mathematics. Students should be exposed early to the notion that mathematics is a creative endeavour, not just an application of supposed ‘right’ thinking. Of course, from the teacher’s perspective, grading the students’ answers to such a problem can become nightmarish. However, it is not the point of a test to make it easy to grade; the point of a test is to test the student, as questions like this can do admirably.

MrHonner · July 30, 2013 at 11:33 am

It’s certainly important to pose questions to students that encourage them to think creatively and interpret mathematics in their own way. This, however, is not such a question, and standardized exit exams are not the place to ask them.

Hao Ye · November 23, 2013 at 5:06 am

“The truth of the matter is that real mathematics, as practiced everyday by professional mathematicians, often has to break with rules “in neat little boxes”, and just plow through with ‘mindless’ symbol manipulation without regard as to validity of the intermediate steps, only afterwards is justification sought or even warranted.”

I emphatically disagree with this.

For people who use mathematics with real-world applications, it can be very dangerous to not check if intermediate values are complex (much less negative). If your bank offers to quadruple your interest rate for a one-time flat fee, what do you want it to do if that flat fee is more than your current savings?

(a) start growing your debt at an increased rate
(b) keep your account at 0 with a constant amount owed
(c) tell you you can’t take part because you can’t pay the fee upfront

Now imagine it’s a company programming flight control software or an engineer designing a bridge. BAD things happen when you don’t check for domain issues.

Furthermore, for actual math professors who do research, mathematical rigor is absolutely crucial. Maybe it is not necessary to check every step when first approaching a problem, but if you try to publish a result without an actual proof (or strong statistical evidence), you won’t be taken seriously.

Math Skills Coach · November 23, 2013 at 12:23 pm

I agree with all of you that, at some stage rigor is necessary, but we give students the wrong impression of mathematics if we tell them that they must just apply rules to do mathematics, as if they were bookkeepers or accountants. It must always be creativity first, rigor second. Very little progress would ever be made in mathematics if rigor were the most important skill to learn.
Simple example: solving linear differential equations using the characteristic polynomial came about when the differential operator was treated as a simple variable, factored out, set to zero, and the roots found. This method was only justified much later.
Another example: the calculus as invented by Newton and Liebniz. It took a couple of centuries for full justification.

Math Skills Coach · November 23, 2013 at 1:27 pm

Of course, what I really meant to say was: discovery first, rigor afterwards.

Have you ever given any thought to how imaginary numbers came about? It was in a situation much like we have here. At some stage in a calculation, a square root of a negative was found. Now quitting the calculation and muttering that something has gone seriously wrong is one option. The other option is to ask,”what if we just continued?” And lo and behold, after some more manipulation, the root of the negative disappears, and a “real” result obtains. That is the kind of blue sky thinking, asking what if?, plowing through that must be encouraged in our students.

Yes, all mathematics needs to be rigorous,…eventually. Scarcely anything new will be found if we blindly adhere to rules.

As to the point that this was a test question, thus only a review of learned material is warranted. During a normal lecture, normally less than half a student’s attention is engaged, but during an exam, a student is fully (or as close to fully as you’re ever going to get) engaged. Talk about a teachable moment! Personally, I have always felt disappointed walking away from an exam where I didn’t learn something new. In fact, if a student doesn’t learn something new for every moment that you’ve got their attention, you’ve wasted their time as a teacher.

K Yang · July 31, 2013 at 1:15 am

I called the state regarding this question. The representative told me that even though 10 is not in the domain of the (real-valued) function, “we can plug in whatever we want because it’s a function.”

Iwan · August 11, 2013 at 7:22 pm

I am shocked by the explanation of the rep above.

MrHonner · August 11, 2013 at 8:46 pm

This sort of thing would be more surprising to me had it not happened before.

There is a good account of an infuriating back-and-forth with the state about an absolutely embarrassing question here: http://jd2718.org/2011/06/23/ny-state-backs-down-on-inverse-flub-no-geometry-gaffes-until-later-today/

Math Skills Coach · November 23, 2013 at 9:57 pm

To be honest, if I were marking this question, full marks would be given for either of the proposed solutions. This whole matter amounts to a clash of cultures between logicians (no square roots of negatives when working in the reals) and mathematicians (simplify the expression as much as you can, then determine where it holds.) Freshman calculus students would typically be instructed to apply the exponent, thus getting rid of the square root, then to simplify before considering the question of domain. This would be part of a general method whereby composition of functions would be enacted through substitution, followed by simplification and then the domain would be ascertained only for the final expression. Why is it taught this way, when we know that this contradicts the abstract theory of functions? The short answer is that the theory of functions is only a tool, to be used or not used with discretion. I provide a longer answer below.

About a century ago, due to several crises in the foundation of mathematics brought on mainly due to the much earlier invention of the differential calculus, it was decided that all mathematics should be derived from logic, essentially making mathematics a branch of logic. Russell and Whitehead produced a huge body of work attempting this feat. Later, through the work of people like Godel, it was shown that such an attempt would fail. Since then mathematicians and logicians have largely inhabited different worlds. This is not the whole story, however.

Another thread in this story is the mere fact that problems in mathematics are often not posed in an ideal manner. Only when the solution is obtained do we realize what we really should have been asking. As well, methods that avoid things like roots of negatives or other unpleasantries, are far more cumbersome than necessary – using quick and dirty tricks will get you the desired answer, at a ‘smaller’ cost.

Mathematical problems do not fall out of the sky, to be solved exactly as given. They are formulated for a specific purpose, and often formulated badly at first. A good student doesn’t just solve the problem as given, but questions why and how the problem is asked, if necessary, even re-formulating the problem. Many teachers are too cynical to give students credit for thinking in such innovative ways.

It is very important to remember that once a proof of a formula is obtained, the mathematician’s work is not done. I won’t go into details here, but recently I saw a proof of a formula by mathematical induction. Obviously, the formula is then only valid for positive integers. Not so! By using the ‘finitude’ of the formula, and the ‘infinite presence’ of the positive integers in the reals, it was shown that the formula was valid for all reals – and might even be extended to complex numbers, once we know what the meaning of that would be. There is even a method popularized by Herbert S. Wilf called “Proof by Example.” How often have we told students that one example does not suffice to prove a theorem in general? Well it turns out that, sometimes, a well-chosen example, does suffice.

Instances of ‘rule-bending’ abound in mathematics: take, for example, the umbral calculus, reputedly so named for the ‘shady’ methods it employs. There are also more prosaic instances. Often we use diagrams to motivate a problem, where an unknown distance might represent a real number quantity. When we solve the problem algebraically, one of the solutions may turn out to be negative, surely a throw-away. Sometimes not. A careful re-interpretation of the problem sometimes gives meaning to such a solution.

It is still much harder to ask the right question in mathematics than to answer that question. That is why a question should not be given an independent existence, automatically leading us to the right answer. A question is only a starting point to encourage exploration. Often we find that, in the end, the question deserves no answer – it becomes irrelevant.

It helps to remember that universal education was first set up to properly prepare children (actually boys then) to enter the military. Recruits were found to be too unruly, not disciplined enough, and lacking basic literacy. Universal education was to be the remedy. Later corporations found that getting children to march in formation was excellent preparation for the factory and office. However, times have radically changed. Strict conformity and adherence to rules for their own sake will just not cut it anymore. In today’s entrepreneurial world, everyone must march to the beat of their own drum. It is no longer the role of the teacher to instill ‘right thinking’ in students. Students must be encouraged to think and act for themselves. This means, that even in mathematics, I hope that I have convinced you, there is not just one ‘right answer,’ It has actually been this way ever since the first herdsmen used pebbles to keep count of their sheep, but the previous, now irrelevant, demands of government and industry, had temporarily altered perceived reality, and certainly for far too long. I am not saying that the needs of government and industry no longer matter in education, only that those needs have changed with technology and society, and that many more of our students are destined to make paths that do not lead to employment but to entrepreneurial ventures instead.

So, yes, I would be happy with either answer. They are equally correct, much like those two roads that lay equal in that famous Robert Frost poem.

l hodge · November 30, 2013 at 3:13 pm

Is root(-1) defined as “i” in the “curriculum”?

Initially we think of the square root symbol as meaning the “positive” square root of a positive number. But, what does it mean to be a “positive” square root of a negative or complex number?

Tanton has some interesting commentary on this. In particular the breakdown of the usual square root rules. Something along the lines of: -1 = i x i = root(-1) x root(-1) = root(-1 x -1) = 1.