Regents Recap — June 2013: Solving Quadratic Equations
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
Solving equations is a fundamental mathematical skill, and it makes sense that we emphasize it in school curricula. And since quadratic functions come up quite a bit in mathematical and scientific exploration, and offer a good balance of accessibility and complexity, it makes sense that solving quadratic equations is a particular point of emphasis.
This June, each of the three New York math Regents exams had at least one problem that required the student to solve a quadratic equation. I don’t really have any objection to this, but what I find strange is the implied gap in mathematical content suggested by the types of questions asked.
Consider the following two questions. The first is from the Integrated Algebra exam and the second is from the Algebra 2 / Trig exam. These two exams, and their corresponding courses, are typically taken 2-3 years apart.
The only difference between the content of these questions is the nature of the solutions of the equations. In the first, the solutions are integers; in the second, the solutions are irrational numbers. Thus, students are taught to solve quadratic equations with integer solutions in the Integrated Algebra course, but it isn’t until at least two years later that they are taught to solve quadratic equations with non-integer solutions.
That seems like an unreasonably long gap to me. I’m not sure what the reasoning is behind waiting 2-3 years to teach students how to solve more complicated quadratic equations. Maybe someone can make a sensible argument for this pacing and structure, but I’m not sure I can.

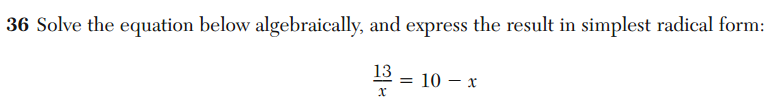
4 Comments
Mike Lawler · July 19, 2013 at 9:24 am
I’m really enjoying your posts about the questions on these exams. Hopefully your work will inspire other people to do some critical analysis of the exams.
For the two questions you’ve studied in this post, the fact that one is multiple choice and the other is not is an important difference. Even if you know nothing at all about how to solve quadratic equations, you can still find the correct answer to the first question by just plugging in the choices. In fact, this approach will probably lead to a quicker solution even if you do know how to solve quadratics.
I’d argue that the first questions is at least as much of a measure of a student’s skill at taking multiple choice tests as it is of the student’s mastery of quadratic equations.
MrHonner · July 19, 2013 at 10:04 am
Mike-
When comparing these particular questions, I agree that the difference in question type is significant. But the point I’m making here is about what these questions say about the curricula of the corresponding courses.
It’s not as though students in the Integrated Algebra class are only taught to solve quadratics by plugging in and checking possible answers. Although untested by the above problem, they are indeed taught to put an equation in standard form, factor, and apply the zero product property to find the solutions. But it isn’t until 2-3 years later that a student learns what to do if the quadratic can’t be factored nicely. That just doesn’t seem right to me.
Mike Lawler · July 20, 2013 at 7:27 am
The 2 to 3 year gap from start to finish on quadratic equations does not seem right to me either.
I checked the series that I’m following with my kids and here is how quadratics are presented (you can see the complete table of contents here – http://www.artofproblemsolving.com/Store/products/intro-algebra/toc.pdf) :
From Art of Problem Solving’s Introduction to Algebra book –
Chapter 10 – Quadratic Equations part 1
Even this chapter has square roots. For example problem 10.58 in the Challenge problem section asks which is larger \sqrt{2} or 2*\sqrt{3} – 2
Chapter 11 – Special Factorizations
Also lots of problems with square roots in this chapter, including rationalizing denominators (!)
Chapter 12 – Complex Numbers
Obviously square appear in this chapter.
Chapter 13 – Quadratic Equations part 2
The quadratic formula appears here as well as some wonderful challenge problems. The last problem in this chapter is:
Compute the number of positive integers “a” for which there exists an integer “b”, 0 <= b <= 2002, such that both of the quadratics "x^2 + ax + b" and "x^2 + ax + b + 1" have integer roots. Source: ARML
Chapter 14 – Graphing Quadratics
So, just glancing through the approach in Art of Problem Solving, I really like their approach. By coincidence, we closed the book at Ch 9. this spring with my older son, so I'll be following these chapters this fall. These 5 chapters are covered in about 150 pages. I expect that will take us from September through December as we sort of plod along. Certainly the 2 to 3 year gap you mention seems way too long.
MrHonner · July 21, 2013 at 7:55 am
I also like the AoPS books. They are a bit inconsistent in quality, but generally they are a great resource for both teachers and students. And they are probably the best option out there for advanced students wanting to consume a lot of extra mathematics.