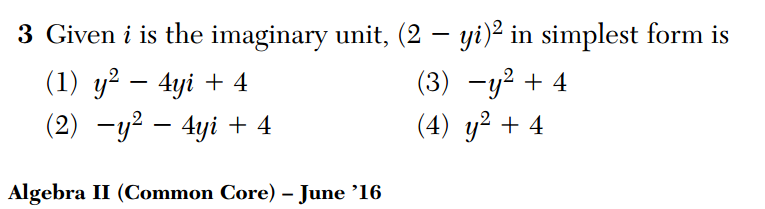I read this problem several times and still did not understand what it was asking for. It is the first part of problem 36 from the June 2016 Common Core Geometry Regents exam.
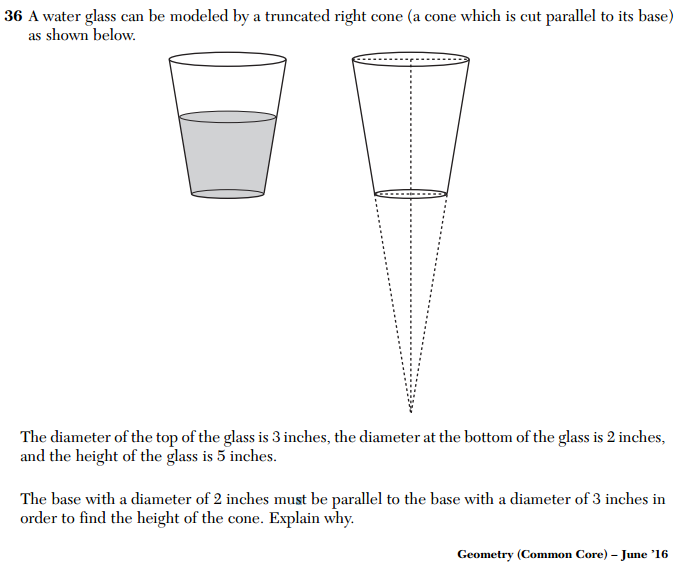“The base with a diameter of 2 inches must be parallel to the base with a diameter of 3 inches in order to find the height of the cone. Explain why.” Explain why? What do they want to hear?
Is the expectation that students will say something like “Height is only well-defined when measured between two parallel objects”, or “If the bases aren’t parallel, the height will vary depending on where the measurement is taken, thus height is only a meaningful measurement when the bases are parallel”? As usual, the rubric was no help, simply awarding points if A correct explanation is given.
But the model student work says it all. Here are two examples of complete and correct solutions.
These are not explanations of why the two bases must be parallel. These are descriptions of how you might compute the height given that the two bases are parallel. This argument essentially says “The bases are parallel because in order answer this question I need to apply a technique that requires that the bases be parallel.”
Not only is this not an explanation, it’s a kind of argument we want to teach students not to make. Validating these responses works against what we should be trying to do as math teachers.
These high stakes exams shouldn’t encourage teachers to promote invalid mathematical thinking. Unfortunately, as the posts below suggest, it’s happening far too often.
Related Posts
- Regents Recaps
- Regents Recap — January 2015: It’s True Because It’s True
- Regents Recap — August 2015: Modeling Data
- Regents Recap — June 2014: Common Core Algebra, “Explain your answer”
and 
are representations of the same number, the first fraction is likely to be seen as simpler than the second. But if the goal were, say, to determine if the number was greater than 
, then the expression on the right might be considered simpler.