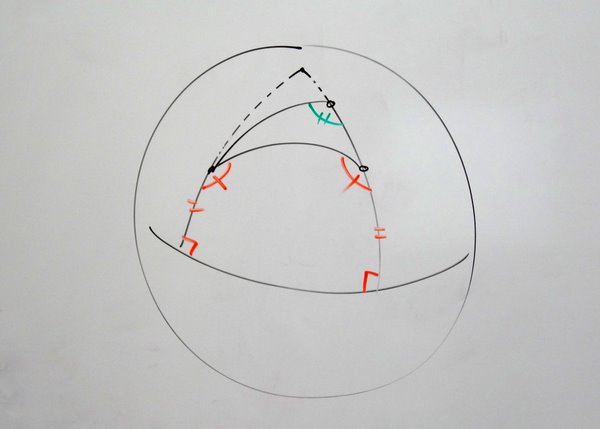
We’ve been exploring non-Euclidean geometries lately, and the Saccheri Quadrilateral plays a pivotal role in this particular mathematical history.
The Saccheri quadrilateral is a biperpendicular quadrilateral with two congruent legs. It’s an object that is “obviously” a rectangle in Euclidean geometry, but proving that without the aid of the parallel postulate turns out to be rather tricky.
In fact, just proving that the measure of the green angle is less than the measure of the orange angle is pretty tough!