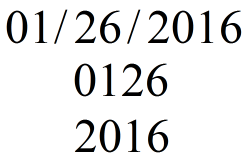Next stop, Perpendicular?
Appreciation Numbers
02/16/2016 — Happy Permutation Day!
Today we celebrate the second Permutation Day of the year! I call days like today permutation days because the digits of the day and the month can be rearranged to form the year.
We can also consider today a Transposition Day, as we need only a single transposition (an exchange of two numbers) to turn the year into the day and date.
Celebrate Permutation Day by mixing things up! Try doing things in a different order today. Just remember, for some operations, order definitely matters!
Appreciation Numbers
01/26/2016 — Happy Permutation Day!
Today we celebrate the first Permutation Day of the year! I call days like today permutation days because the digits of the day and the month can be rearranged to form the year.
Celebrate Permutation Day by mixing things up! Try doing things in a different order today. Just remember, for some operations, order definitely matters!
Appreciation Geometry
Math Photo: A 26-gon
Thanks to the strong presence of mathematicians and math teachers on social media, I know I’m not the only person who, when sitting around with a box full of compasses, unexpectedly ends up doing things like this.
A circle made of circle-makers! Or, from another perspective, a regular 26-sided polygon.
The fact that I created an object that doesn’t even appear to have a name made me feel a little better about this use of time.
Appreciation Art Numbers
Happy 2016!
In honor of the new year, here’s the complete graph on 64 vertices, with its 2016 edges!
A complete graph is a graph in which every pair of vertices is connected with an edge. In a complete graph with n vertices, there are
edges. The above graph has 64 vertices equally spaced around the perimeter. Thus, , and we have
edges.
The number 2016 is special for a variety of reasons. For example,
So 2016 is equal to the sum of the first 63 positive integers! This makes 2016 a triangular number, a fact beautifully demonstrated by David Swart in this image.
And John D. Cook illustrates the combinatorial nature of 2016 by pointing out that this is the number of ways to place two pawns on a chessboard!
However you think of it, 2016 is a pretty great number! And here’s hoping 2016 is a great year.