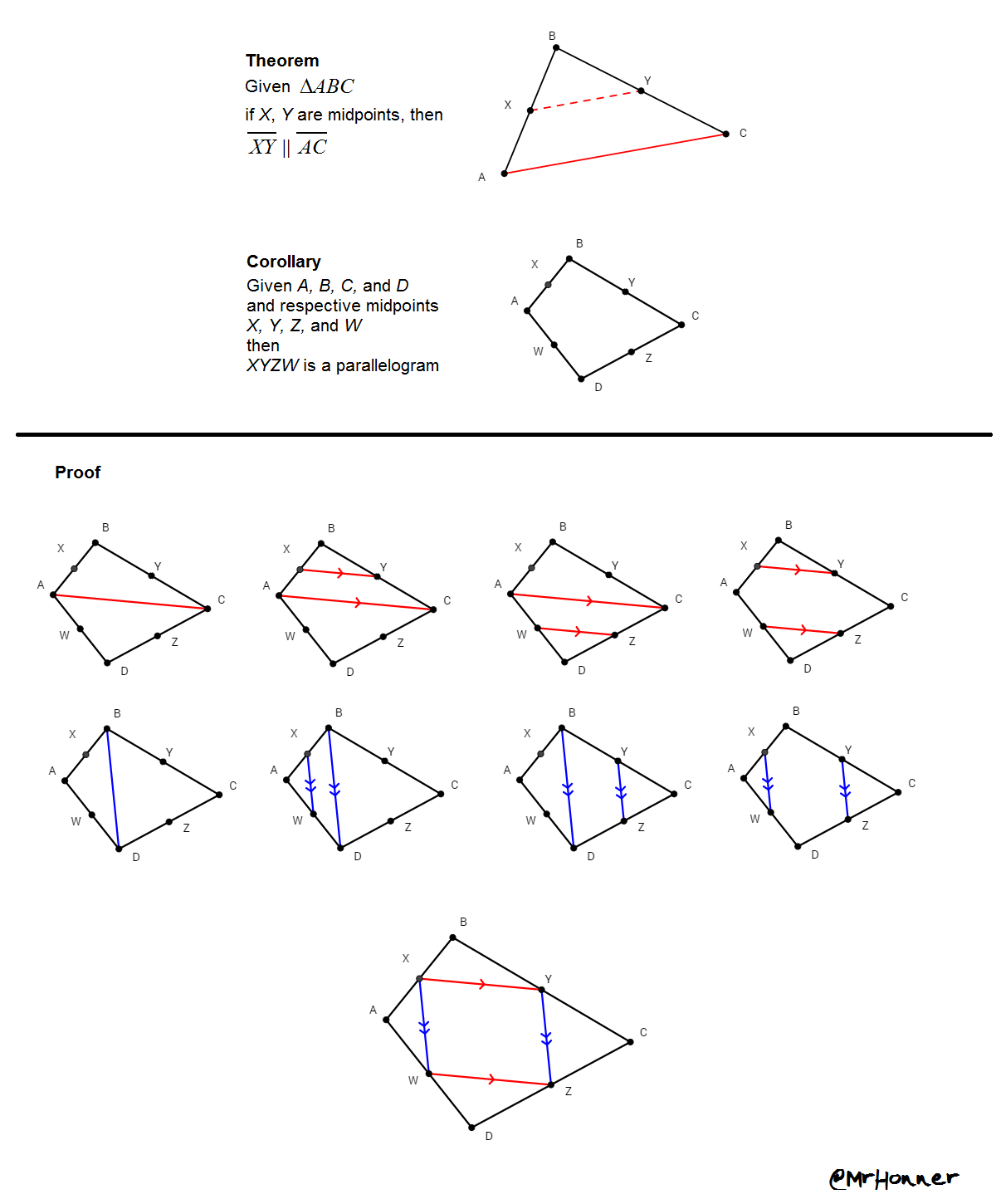
Varignon’s Theorem
Varignon’s Theorem is one of my favorite results in elementary geometry: connect the adjacent midpoints of the four sides of any quadrilateral, and a parallelogram is formed! It is a magical result that defies expectations, and it’s so much fun to play around with, explore, and extend.
Steven Strogatz shared his favorite proof of Varignon’s Theorem on Twitter yesterday, and so I felt compelled to share mine. This is a standard proof of Varignon, but it is so clean and elegant: it is an immediate consequence of the Triangle Midsegment Theorem and the transitivity of parallelism.
Strogatz’s vector proof is beautiful and efficient, but the power of transitivity really shines in this elementary geometric proof.
I created a a simple Desmos demonstration to explore Varignon’s Theorem. And like all compelling mathematical results, there are so many fascinating follow-up questions to ask!
Related Posts
3 Comments
Jonathan Halabi · August 18, 2016 at 11:16 pm
Coordinate proofs of this are clumsy, but I find them rather satisfying.
But yes, I prefer yours.
And nothing changes for the non-convex cases. That sometimes gets an ooh from the kids.
MrHonner · August 19, 2016 at 7:09 am
I enjoy the coordinate connection here, as well, but I generally wouldn’t lead with coordinate proofs of results. In fact, I teach all coordinate geometry at the end of the course.
And even more mind-blowing is that the result, and the proof, is valid even if the four points aren’t coplanar!
Jonathan Halabi · August 19, 2016 at 2:41 pm
Took me a moment to digest that! Each triangular is in a single plane. The midsegments are parallel to the same base, and (transitive) each other. And if two distinct lines are parallel, they are contained in one plane. Nice. Thank you!