Regents Recap — June 2013: Where Do Systems Belong?
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
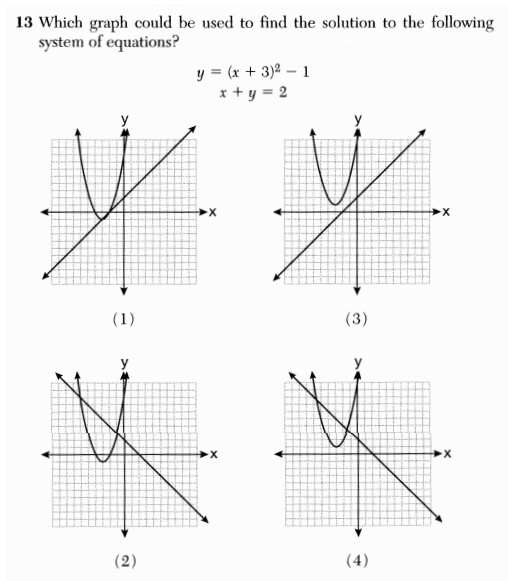
Consider the following three questions from the June 2013 New York math Regents exams.
From top to bottom, these questions appeared on the Integrated Algebra exam, the Geometry exam, and the Algebra 2 / Trig exam.
Solving systems of equations is a fundamental mathematical skill and should be a part of any math course. But do these three questions really span 3-4 years of mathematical learning?
The first two are simply different representations of the same problem. The third question involves a relation instead of a function, but it’s presentation as a multiple choice question sidesteps any additional algebraic or geometric complexity that dealing with a relation might entail. Ironically I think the question from the earliest exam is the hardest of the three.
I’ve written about this curious treatment of systems of equations in analyzing other Regents exams. This phenomenon comes to mind when politicians and administrators take credit for raising test scores, or trumpet gains in student growth from year-to-year.
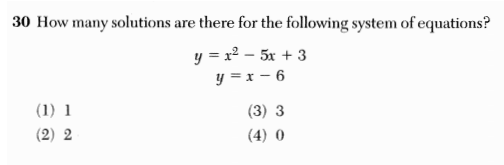
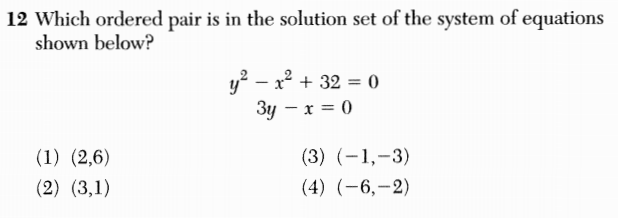
3 Comments
Five Triangles · July 17, 2013 at 3:59 pm
Agreed the Integrated Algebra problem is the hardest; the Algebra 2 problem could be solved by a middle schooler without knowing anything about hyperbolas. It certainly seems clear that, in your ongoing exposé of Regents’ many inconsistencies and redundancies, the committees that design each test don’t communicate with each other.
We wonder what the future holds in store. Common Core first covers non-linear systems with one linear and one quadratic function in A-REI.7, so it seems that future Regents exams could test it in Grade 9, but PARCC may also test systems in Grade 11, since assessments should cover years 9-11.
Another standard, F-IF.9, seems to revisit systems, but in an odd way, where one function could be already graphed; the other written as a table of values. That’s what PARCC attempts to align with in one of its officially released questions:
http://www.parcconline.org/samples/mathematics/high-school-functions
***
As is our habit, we’ll plug a problem of the caliber we’d like students to be tackling:
http://fivetriangles.blogspot.com/2012/04/quadratic-functions.html
Christian Perfect · July 22, 2013 at 1:04 pm
Are all the questions multiple choice? The third one is egregious, but I can think of a few plausible but wrong answers to the first one that the student can’t give, which might lead to them getting the right answer for the wrong reason. I’m sure you’ve discussed the badness of multiple choice before, anyway.
It’s interesting that the third one only implies that the pairs are of the form (x,y), and not (y,x). I doubt any student would actually think it’s (y,x), but I also don’t think I’d write “(-6,-2)” as my solution instead of “x=-6, y=-2” unless I’d also drawn a graph.
MrHonner · July 22, 2013 at 1:49 pm
Each test has a multiple choice section and a free response section. Obviously these problems appeared in each test’s respective MC section.
There are good multiple choice questions out there, but not on these exams.