Appreciation

This October I had the great pleasure of meeting Fields medalist Cedric Villani. Professor Villani gave an illuminating and accessible talk about his innovative work in the study of curvature, and afterwards spent some time hanging out and chatting with a few of the attendees.

Villani is a charismatic and engaging speaker, and he provided a lot of to think about in his talk. One remark that particularly struck me was

“Mathematics, in some sense, will always involve a little pain.”

The idea resonated with me but I was curious what he meant, so I asked him about it. I was a bit surprised when he said that mathematics is unnatural, and unnatural things are always painful.

I pressed him a bit, as I didn’t quite understand. “What are the first things you learn in physics?” he asked. He was alluding to Newton’s Laws, and in particular the law of inertia: An object at rest tends to stay at rest, and an object in motion tends to stay in motion. Villani grabbed a fork from across the table, slammed it down in front of him, and gave it a push. The fork slid a short distance and stopped. “This is absurd!” he said. “It does not stay in motion!”

Physics, that is, the laws of physics, are abstractions of our experiences with the real world. Understanding that when you push something, it will stop, is natural for us; understanding the law of inertia is not. This law is an abstraction of our natural experiences, and as such, is unnatural. He went on to argue that mathematics, too, is a collection of abstractions from our experiences of the real world, and therefore is unnatural.

He made an analogy with speaking and reading: speaking is natural for humans, we are hard-wired for it. But writing is not. It does not come naturally to us. As an abstraction of speaking, writing will always be difficult for humans to learn. It will always involve a little pain. Like mathematics.

Some world-class mathematics, a little philosophy, and a mathematical autograph! All in all, a pretty good evening.

By MrHonner, 11 years4 years ago

Appreciation Geometry

12/5/13 — Happy Right Triangle Day!

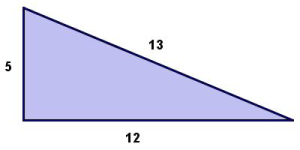
Happy Right Triangle Day! Today we celebrate a favorite geometric object: the 5-12-13 right triangle.

Of course, the sides of this triangle satisfy

$5^2 + 12^2 = 13^2$

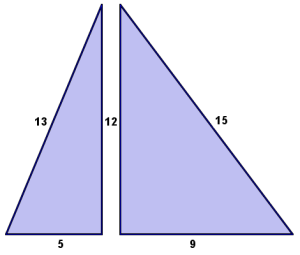
and, thus, form a right triangle. But one reason I like this particular right triangle so much is the role it plays in another favorite triangle. The 5-12-13 triangle fits together perfectly with the 9-12-15 right triangle

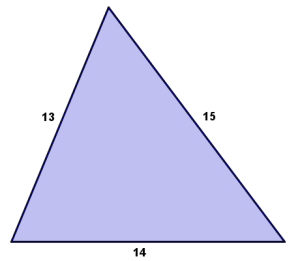
to make the 13-14-15 triangle!

The 13-14-15 triangle is special in its own right: it is a Heronian triangle, a triangle with rational side lengths and rational area. In fact, this triangle has integer side lengths and integer area, making it especially interesting!

Happy Right Triangle Day! If you’re in New York City, you might want to join the Museum of Math as they pythagorize the Flatiron Building!

By MrHonner, 11 years9 years ago

Appreciation Numbers

12/03/2013 — Happy Permutation Day!

Today we celebrate a Permutation Day! I call days like today permutation days because the digits of the day and month can be rearranged to form the year.

Not only is today a permutation day, but it is also a double-transposition day! We can turn the month and day into the year by first transposing the ‘1’ and the ‘2’, and then transposing the ‘1’ and the ‘0’. Permutation days are also nice because, unlike Palindrome days, they can celebrated on both sides of the Atlantic without heated disagreement.