Each Math Research Project outline consists of a Seed Question, Questions to Build On, Extensions, and Basic Background.  Click here to see a list of available Math Research Project outlines.

The Seed Question is a question that appears in a typical math curriculum.  Questions to Build On are simple extensions, re-interpretations, and generalizations of the Seed Question that a student can build a simple math research paper around, with help from a mentor (be it student or teacher).

The Extension Questions are bigger, more challenging extensions of the Seed Question.  If a student can make some headway into understanding these, great!  If not, they are good questions to include as part of the “Where do we go from here?” section of the paper.

The Basic Background consists of some of the mathematical leg-work that underlies the investigation.  It can be worked on simultaneously with the investigation, which gives it context

.

Project Idea:  Midpoints and Beyond

Seed Question

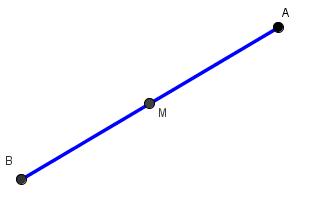Find the midpoint, M, of the segment with endpoints A(3,1) and B(15,9).

Questions to Build On

The midpoint M divides the segment AB into two congruent segments.  What are the coordinates of the three points that divide segment AB into four congruent segments?

What are the coordinates of the two points that divide AB into three congruent segments?

Find the point on AB that is twice as close to A  as it is to B.  Are there any other such points, say, not on AB?

Find the point on AB that divides AB into segments whose ratio is p/q.

Extension Questions

Find the midpoint of P(1,4,10) and Q(-3, 2, 4).

The midpoint of M of AB is equidistant to A and B.  Find all points in the plane that are equidistant to A and B.

Find all points in space that are equidistant to P and Q.

What is the “midpoint” of three points in the plane?

Basic Background

Derive the distance and midpoint formulas.

Verify that AM = BM using the distance formula.

Verify that AM = BM by constructing two congruent right triangles with AM and BM as respective hypotenuses.

Click here to see a list of available Math Research Project outlines.