Search Results for: mastodon

Teaching

Revolutionary Ideas in Math Education

I saw some dispatches from the NCTM (National Council of Teachers of Mathematics) annual meeting this past week, and I’m always disappointed at what constitutes professional discourse in math education. Beyond the facile messages of “thought leaders” and influencers, even the messages of purported substance seem like a continual re-telling of what should be obvious to everyone. Get students doing mathematics. Engage them intellectually and socially. Pay attention to how they think. These should not be revolutionary ideas.

Originally posted on Mastodon.

By MrHonner, 2 months2 months ago

Teaching

Taught Helplessness

I’m currently reading “The Design of Everyday Things” by Don Norman and it’s interesting to think about what the theory of product design has to say about instructional design.

For example, the author discusses how “learned helplessness” can result from poor design. A product whose functionality isn’t discoverable, and that doesn’t provide good feedback, will be frustrating to use, so users will likely give up after trying and failing a few times.

Just as I was making the connection to teaching math in my mind, the author himself brought up math instruction as a common example of “taught helplessness”: When math is presented as unintuitive, and poor or misguided feedback is given, students are likely to just give up. The problem is amplified by the linear way in math is usually taught. In many classrooms, if you don’t understand what happened yesterday, you will probably struggle to understand what is happening today.

Originally posted on Mastodon.

By MrHonner, 11 months11 months ago

Challenge Numbers

2024 and Differences of Squares — Solution

The new year 2024 is a difference of squares, $2024 = 45^2 - 1^2$ , which got me thinking about a fun little number theory problem:

Is there a largest number that can not be expressed as the difference of squares? If so, find it. If not, prove no such number exists. Good luck, and happy new year!

As promised, here’s my solution.

There are infinitely many numbers that can not be expressed as a difference of squares. In fact, we can completely characterize numbers that can be expressed as a difference of squares and those that can’t. It all starts with factoring.

Differences of squares have a useful structure that can be exposed by factoring:

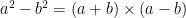
$a^2 - b^2 = (a + b) \times (a - b)$

We can leverage this structure to answer our question.

Suppose n can be factored as $n = s \times t$ . If n can be expressed as a difference of squares, then we can also write

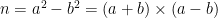
$n = a^2 - b^2= (a + b) \times (a - b)$

Now set $(a + b) = s$ and $(a - b) = t$ . This gives us the system of equations

$a + b = s$

$a - b = t$

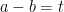
We can solve this system by adding and subtracting the equations. Adding gives us $a = \frac{s+t}{2}$ , and subtracting gives us $b = \frac{s-t}{2}$ . This shows us how to express n as a difference of squares: Just factor n into $s \times t$ , compute $a = \frac{s+t}{2}$ and $b = \frac{s-t}{2}$ , and then $n = (a + b) \times (a - b) = a^2 - b^2$ .

There’s only one thing we have to worry about: a and b must be integers. But as long as s and t have the same parity — that is, s and t are both even or both odd — then the sum and difference of s and t will both be even, and so $\frac{s \pm t}{2}$ will be an integer.

This means that n can be expressed as a difference of squares if and only if we can write $n = s \times t$ where s and t are both odd or both even. This is usually possible, often in multiple ways. But there’s one situation when it isn’t: When n is divisible by 2 exactly once. When this is true, then however you factor n into $s \times t$ , the lone factor of 2 will end up as a part of either s or t, making one of them even and the other odd. Thus, in this case, it’s impossible to factor n so that the two factors have the same parity, and so it’s impossible to express n as a difference of squares.

This gives us a complete answer to our question: A number n is not expressible as a difference of squares if and only if it is divisible by 2 exactly once! In other words, every odd number times 2 is not expressible as a difference of squares, and every other integer is.

As an example, given $n = 105 = 3 \times 5 \times 7$ , we can factor $105 = 7 \times 15$ which gives $a=\frac{15+7}{2}= 11$ and $a=\frac{15-7}{2}=4$ , and sure enough, $105 = 11^2 - 4^2$ . Notice, we could also write $105 = 5 \times 21$ , which gives $a = \frac{21+5}{2}=13$ and $b = \frac{21-5}{2}=8$ , so $105 = 13^2 - 8^2$ .

On the other hand, it isn’t possible to do this at all for 6. There are only two factorizations, $6 = 6 \times 1$ and $6 = 2 \times 3$ , and in both cases the factors have different parity, so the a and b we need won’t be integers.

There’s an interesting resemblance here to Euclid’s Formula for generating Pythagorean triples. There’s also an interesting follow-up question about how many different ways a number can be expressed as a difference of squares. And since the numbers that answer our question are those that are divisible by 2 exactly once, I wonder what properties numbers that are divisible by 3 exactly once have.

Thanks to everyone who contributed on the Mastodon thread! There are some cool ideas there as well, so be sure to check it out.

Related Posts

By MrHonner, 11 months11 months ago

Resources Writing

Books I Read in 2023

Here’s a selection of books that made an impact on me in 2023.

Superforecasting tells the story of psychologist Philip Tetlock’s project to systematically evaluate the predictions of experts. What exactly does an advisor mean when they tell the President that a military operation has a “good chance” of being successful? It wasn’t so long ago that no one thought to even ask such a question, and as Tetlock shows, the consequences couldn’t be more real. Tetlock’s work led to the development of the Good Judgement project, a forecasting competition designed to identify the characteristics of “superforecasters”, individuals with a quantifiable talent for predicting how world events will unfold. It’s a great book, and one I was partly inspired to read because of my involvement in a student forecasting tournament based on the Good Judgement project (where our students took first and second place overall!)

I finally read The Lady Tasting Tea, by David Salsburg, which had been on my list for a while. It’s an excellent history of the development of statistics, told through fascinating characters and interesting anecdotes. It immediately joined my student lending library, and it also took second place on the list of statistics book I’ve learned the most from (to be fair, it’s first on the list of books I’ve learned from by reading it rather than writing it). It’s full of fun little details, like this quote I shared with my linear algebra class the very day I read it.

Manil Suri’s The Big Bang of Numbers was a highlight of my year, both because it’s a unique book that tells a whimsical origin story of mathematics full of insight, humor, and even spirituality, and also because I had the privilege to interview Manil Suri at the Jaipur Literature Festival this past year (video here).

Made to Stick, by Chip and Dan Heath, is the book that I’ve been thinking most about as a teacher this year. Why do silly ideas go viral while important ideas struggle to take hold? It’s a question every teacher should consider, and Made to Stick offers lots to think about. Months later I’m still pondering the power of generative metaphors, story as simulation, and why people should care about duo piano. Thanks to my (former) student Satvik for the recommendation!

Atomic Habits by James Clear was another book that had been on my list, and it was a worthwhile read even if confirmed many previously held beliefs. A core idea of the book is very mathematical, namely that the impact of habits compound like interest in a bank account, generating exponential (hopefully, positive) personal growth.

I feel a bit funny saying that John Fleischman’s Phineas Gage was probably the best book I read this year, seeing as its target audience is middle school students. But this infamous story of the 19th-century man who blasted a railroad spike through his brain and lived to tell about it is so vivid, engaging, and expertly contextualized in the history of science that it keeps coming up in thoughts and conversations.

In fiction, I enjoyed Susanna Clarke’s Jonathan Strange and Mr. Norrell, a fantastical history of magic in Britain told through the story of the apprenticeship-turned-rivalry of the title characters. Amor Towles’s A Gentleman in Moscow was one of the loveliest books I’ve read in a long time. And I enjoyed every moment of Elmore Leonard’s Get Shorty. Leonard also authored the stickiest advice I read in 2023: don’t write the parts that the reader skips.

In addition to getting back to my year-end lists (sorry, 2022) I’ve been trying to be more active on Bookwyrm, the ActivityPub-based social network dedicated to reading and reviewing. You can find me there at phonner.

And thanks, as always, to the (shamefully underfunded) Brooklyn Public Library for making it so easy to read this year and every year.

Related Posts

By MrHonner, 11 months11 months ago

Resources Teaching

2023 — Year in Review

As I reflect on my professional 2023 I keep coming back to the line “Normal is normal again.” Not the world, certainly, and not for everyone, but since changing schools nearly five years ago this is the first year when being in the classroom hasn’t felt extraordinary for extraordinary reasons.

Still, it’s been a mix of the new and the old. In addition to my normal lineup of geometry, calculus, and linear algebra courses, I’ve been doing more mathematical modeling with students this year. In the spring we had a team of modelers invited to compete in the International Mathematical Modeling Contest (IM2C), thanks to their excellent work on last year’s High School Mathematical Contest in Modeling (HiMCM), and I’ve been working to expand the program at school. This year interest was high enough to have eight teams compete in the HiMCM, and we’re looking forward to new modeling opportunities this spring. In addition, a colleague and I mentored around 70 students who competed in a national forecasting tournament inspired by the Good Judgement project, and our teams took first and second place!

An extracurricular highlight this year was interviewing mathematician and author Manil Suri for the Jaipur Literature Festival. We had a lively talk about his excellent new book, The Big Bang of Numbers, and also about math, writing, and teaching, and the Asia Society of New York made the entire video of our conversation available here.

As usual, I continued to design and run workshops for teachers this year, including a new entry in my ongoing linear algebra series titled Learning to Love Row Reduction. I also gave two talks at this year’s NCTM Annual Meeting: So, You’re Teaching Pre-Calculus, and A Case for Linear Algebra. I’m already looking ahead to new talks this coming year, including an upcoming workshop on the geometry of linear regression I’ll be presenting in February.

Writing my column for Quanta Magazine was as challenging, and fulfilling, as ever, with pieces aimed at bridging the gap between classroom and research math focused on the newly discovered aperiodic monotile, the algebra of secret codes, graph theory and cliques, a high school student’s amazing proof, and what three-point turns tell us about a hundred-year-old geometry problem.

And with the landscape of social media continuing to change, I’ve been enjoying my time on Mastodon more and more in 2023.

Platforms based on decentralization, user autonomy, and interoperability definitely seem like the right way forward. And I’ve been trying to do a better job of archiving what I write by cross-posting some of my social media posts here on my blog.

It’s been a good 2023, and here’s hoping for another good, and relatively normal, 2024!

Related Posts

By MrHonner, 11 months11 months ago

Search Results for: mastodon

Follow Mr Honner