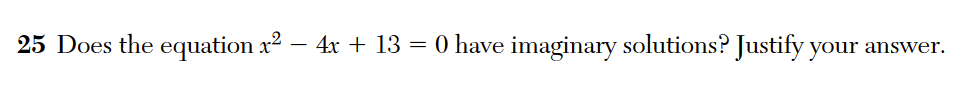Testing

For over 10 years I have been writing and speaking about erroneous math test questions and their consequences. Question 25 from the June 2022 New York State Algebra 2 exam offers a clear and simple picture of those consequences.

The student is asked if the equation has “imaginary solutions”, that is, if the solutions to this equation, 2 +3i and 2 – 3i, are imaginary numbers. These solutions are complex but not imaginary, because imaginary numbers are multiples of i, the imaginary unit. Therefore the answer should be no, this equation does not have imaginary solutions.

As you might have guessed, that’s not the answer they were looking for.

In this “complete and correct” response from the state’s official model response set, the student identifies these solutions as imaginary. These numbers are not real, but they are not imaginary, a subtle but meaningful distinction that neither the student nor the exam creators seem to understand.

Is the distinction important? Maybe not. But what is important is that this student’s lack of understanding of complex numbers will only be amplified by this exam. Even worse, teachers around the state might themselves be confused after reading this model response set. What will they teach their students about imaginary numbers next year?

Worst of all, what about the students who actually do know the difference between imaginary numbers and non-real complex numbers? They’re caught in a trap: Should they give the correct answer and possibly lose points, or should they try to guess what the exam creators really meant to ask? These tests put students in this trap over and over and over again, and ultimately students learn that details don’t matter and that thinking too much is a hazard. Students, and their teachers, deserve better.

Related Posts

• Regents Recaps
• June 2022 Algebra 2 Regents Exam (Twitter Thread)
• g = 4, and Other Lies the Test Told Me
• The Worst Regents Questions of All Time
• Encouraging Bad Habits

On the one hand, it’s good that standardized math tests are trying to include more examples of mathematical modeling, one of the true applications of math to the real world. On the other hand, if these tests promote a false, even dangerous, idea of what a mathematical model is, then they shouldn’t bother trying.

This question from the New York State Algebra 2 Regents exam commits a fundamental error of mathematical modeling: it confuses the model for the phenomenon itself.

Is the maximum depth of the water 12 feet? We don’t know. The model of the water’s depth, d(t), takes a maximum value of 12 feet, but the model is only an approximation of reality. The actual maximum depth of the water is likely to differ from the model, as are the times of high and low tide. We can’t draw specific conclusions like (1), (2), or (4), we can only approximate. This means that all these statements are probably false.

Oddly enough, answer choice (3) seems to understand that models are just approximations, which makes the other answer choices even less defensible. (And all of this ignores the question of whether or not students have the requisite domain-specific knowledge of oceanography to understand what high- and low- tides are.)

In the grand scheme of these exam errors, this is a minor footnote. But as I’ve argued in these posts, and in my talk g = 4, and Other Lies the Test Told Me, these kinds of errors have a cumulative effect of training students to stop thinking when doing and applying math and instead just try to guess what the question writer wants to hear. We should expect more from our assessments.

Related Posts

• Regents Recaps
• June 2022 Algebra 2 Regents Exam (Twitter Thread)
• Regents Recap — January 2018: Problems with Pre-Calculus
• Regents Recap — August 2015: Modeling Data

Completing the square is one of those mathematical techniques that should be taught but probably shouldn’t be assessed on state exams.

First, when you insist that a student use a specific technique to solve a problem, you penalize flexible and creative thinking. Second, completing the square probably isn’t important enough a problem solving technique to warrant its yearly appearance on the New York State Algebra 1 exam.

Of course, the one situation in which completing the square is absolutely indispensable is in deriving the quadratic formula. Which makes this sample student response from the exam’s official scoring materials a bit puzzling.

The student lost a point because, instead of completing the square, they used the quadratic formula to solve this equation. But the whole point of the quadratic formula is that it completes the square for every trinomial. The quadratic formula is completing the square.

As I clarified in comments on Twitter, I find this more amusing than objectionable. But these little windows into the testing process often tell us more about what is valued and understood than test scores themselves.

Related Posts

• Regents Recaps
• Are These Tests Any Good? Part 2

This type of problem frequently appears on New York State Algebra 1 Regents exam.

There’s really no way for an Algebra 1 student to properly “explain” their answer to this question. Proving that a number is irrational is a concept from elementary number theory and is not part of the Algebra 1 course. What the test makers expect is for the student to simply state that a rational number times an irrational number is irrational. Not only is this not an explanation, but such a question reinforces the idea, for both students and teachers, that mathematics is a collection of facts to be memorized and regurgitated.

I’ve written about this issue before, but I didn’t think this kind of problem could get much worse. I was wrong. Here’s an example of a full credit response from the official scoring materials for the 2020 Algebra 1 Regents exam.

In this exemplar full credit response, the student erroneously represents as a number with a terminating decimal expansion, i.e. a rational number. Then the student incorrectly claims that the number 5.19615243 can not be expressed as a fraction and thus must be irrational.

The student has demonstrated some understanding of the situation, but doesn’t grasp the fundamental issue of what an irrational number is. This response shouldn’t get full credit. More importantly, the official scoring guidelines should not communicate erroneous mathematics to those who use them. How many teachers will walk away thinking this is valid? And then teach their students that to show a number is irrational, all you have to do is plug it into your calculator and see if it has eight digits past the decimal point?

This is kind of work that makes this other exemplar full credit response seem not so bad by comparison.

A lively Twitter thread on this problem can be found here.

Related Posts

• Regents Recaps
• Regents Recap, June 2017 : Assessing Irrationality
• Regents Recap — January 2015: It’s True Because It’s True
• g = 4, and Other Lies the Test Told Me