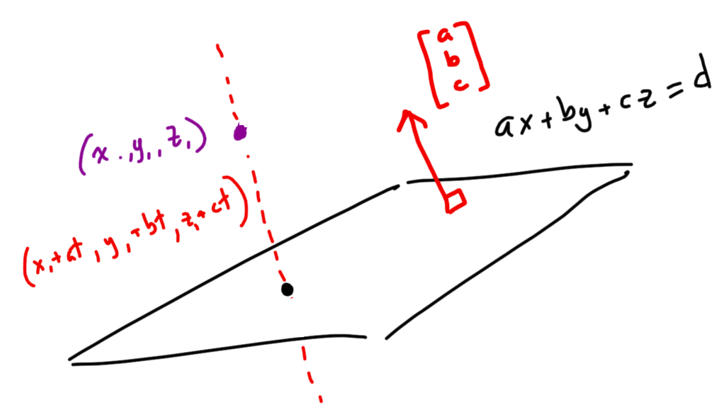
My latest column for Quanta Magazine is about the power of creative thinking in mathematics, and how understanding problems from different perspectives can lead us to surprising new conclusions. It starts with one of my all-time favorite problems:
Say you’re at a party with nine other people and everyone shakes everyone else’s hand exactly once. How many handshakes take place?
This is the “handshake problem,” and it’s one of my favorites. As a math teacher, I love it because there are so many different ways you can arrive at the solution, and the diversity and interconnectedness of those strategies beautifully illustrate the power of creative thinking in math.
By connecting different approaches like counting and recursion, we can connect mathematical ideas across disciplines and discover new relationships.
Like all my columns for Quanta, this piece is free to read at QuantaMagazine.org.