Student Work

Appreciation Student Work Teaching

Math Haiku — Geometry Class, 2016

I personally enjoy writing, and as a math teacher I love getting my students writing about math.

One of my favorite writing assignments for students is math-themed haiku. The rigid constraints of haiku make it an easy exercise, it allows students to access and interact with mathematical ideas in a different and creative way, and the elegance and efficiency of the form evoke the character of mathematics itself.

Here are some selections from this year’s Geometry class. Enjoy!

A rhombtangle A rhombus and rectangle Also known as square	Surface area A polyhedra’s paint job An unfolded thing
Two, the same as two A number equals itself Reflexivity	No definition For a point, a line, a plane At the base of math
As some things, unknown The things we can’t do alone Mathematics lasts	Geometry’s weird Some things just seem to work out So we find out why

Related Posts

By MrHonner, 9 years9 years ago

Art Geometry Resources Student Work Teaching Technology

Using Mathematics to Create — Geogebra

One of my guiding principles as a math teacher, as I articulate in this TEDx talk, is to provide students with tools and opportunities to create with mathematics. Few things are as aligned with that principle as well as Geogebra, the free, open-source, dynamic geometry environment.

I’ve integrated a lot of Geogebra work in my Geometry class this year. I use Geogebra assignments to assess basic geometric skills, to connect old ideas to new, and to explore geometry dynamically.

But much like geometry itself, once you master a few elementary rules in Geogebra, you can create amazing and beautiful works of mathematics.

Below is an example of some wonderful student work from this year. After an introduction to polygons, students were given two simple ideas for creating new objects from polygons: constructing diagonals and extending sides. I gave students some technical tips on how to color and polish their final products, and invited them to be creative. As usual, they did not disappoint.

Students, and teachers, need more opportunities to create with mathematics. We’re fortunate to have technologies like Geogebra that offer us those opportunities.

Related Posts

By MrHonner, 9 years9 years ago

Resources Student Work Teaching

Celebrating Pi Day

Though I would not consider myself a Pi Day enthusiast, Pi Day has become a sort of Mathematical Awareness day, and so I’ve tried to find meaningful ways to observe it with my students.

One aspect of Pi that I try to get students to appreciate is its invariance. It’s not just that Pi is the ratio of circumference to diameter in a circle; it’s that Pi is the ratio of circumference to diameter in every circle. It’s an invariant of circles. And one way I try to get students to appreciate and respect that invariance is by computing “Pi” for other figures.

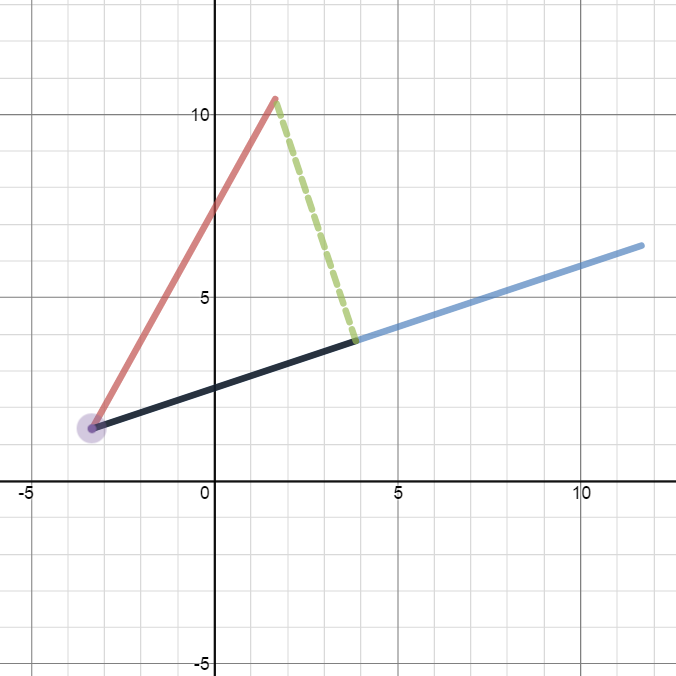
For example, consider the square. The circumference of a square is simply its perimeter. You could choose to consider the red segment below, which is equal in length to a side of the square, as the square’s diameter.

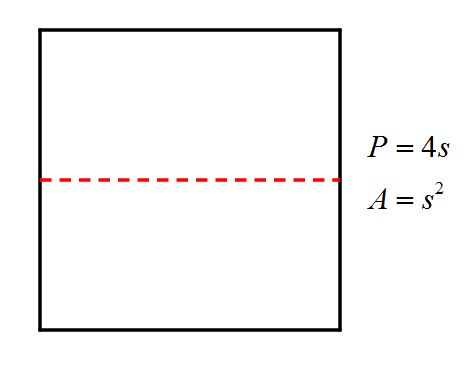
Thus, we can calculate “Pi” for a square to be

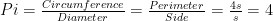
$Pi = \frac{Circumference}{Diameter} = \frac{Perimeter}{Side} = \frac{4s}{s}=4$

Thoughtful students may have other suggestions for the “diameter”, which can be a fun exploration in and of itself. But one way to sidestep this controversy is to simply define “Pi” in a more robust way.

Notice that, in a circle, we have

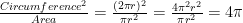
$\frac{Circumference^2}{Area} = \frac{(2 \pi r)^2}{\pi r^2} = \frac{4 \pi^2 r^2}{\pi r^2} = 4\pi$

So we can define “Pi” for any plane figure to be one-fourth the ratio of the square of its perimeter to its area.

This simplifies matters, because area and perimeter are well-defined for most figures, whereas diameter is not. And it’s nice that this new “Pi” is still 4 for a square, since we have

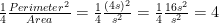
$\frac{1}{4} \frac{Perimeter^2}{Area} = \frac{1}{4} \frac{(4s)^2}{s^2} = \frac{1}{4} \frac{16s^2}{s^2} = 4$

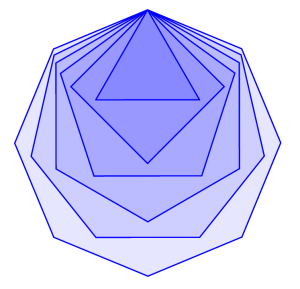
Once students have generalized the notion of “Pi”, there are several interesting directions to go. First, you can explore the value of “Pi” for other regular polygons. What is “Pi” for a regular hexagon? For a regular octagon?

Of course, something wonderful happens as you look at regular polygons with more and more sides. With some elementary geometry and trigonometry to derive the formula for the area of a regular n-gon, you can numerically explore convergence to Pi. And with some knowledge of limits, you can actually prove it converges to Pi!

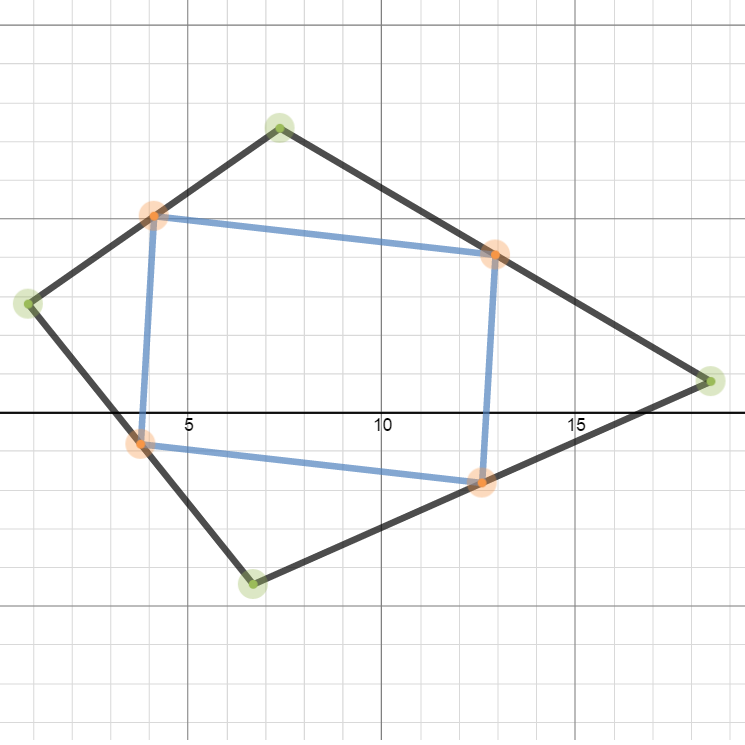
You could also fix n and explore values of “Pi” for irregular n-gons. For example, set n = 4 and compare and contrast “Pi” for different rectangles, rhombuses, and parallelograms. It’s interesting to investigate which kinds of figures have “Pi” values closest to the actual value of Pi. You might even use this idea to develop a metric for equilateralness.

In one of my classes. we took our discussion of “Pi” up a dimension. With help from a Pi Day grant from Math for America, we used Zometool to explore the value of Pi for solids in 3 dimensions.

We built models of cubes, dodecahedra, icosahedra, triacontahedra, and other solids. We debated which solids had “Pi” values closest to the actual value of Pi. Then, starting from the assumption that

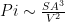
$Pi \sim \frac{SA^3}{V^2}$

we calculated “Pi” for our various solids. Students had a great time with this hands-on activity!

And most importantly, students came away with a better understanding of, and appreciation for, this remarkable constant.

So let’s find meaningful mathematical ways to celebrate Pi Day! Make it a Pi Day resolution.

Related Posts

By MrHonner, 9 years7 years ago

NYT Student Work Teaching

Who Needs Math? A Student Responds

For a political science professor, Andrew Hacker is surprisingly familiar to math teachers. His 2012 New York Times Op-Ed “Is Algebra Necessary?” generated lots of conversation in the math education community, including several pieces from me: “N Ways to Use Algebra With the New York Times” in NYT Learning, and “Replace Algebra with Algebra?”.

Professor Hacker is back in 2016 promoting a new book, and in a recent NYT interview he revives his anti-math arguments from four years ago: math is not really necessary for jobs; it’s too hard; it prevents students from graduating.

I saw the piece and didn’t feel the need to respond. There was nothing new, and I’d said what I wanted to say here.

But I was pleasantly surprised when I saw this letter-to-the-editor, written by a high school student, published in the February 19th edition of the New York Times.

In “Who Needs Math? Not Everybody” (Education Life, Feb. 7), Andrew Hacker, who teaches quantitative reasoning at Queens College, says that since only 5 percent of people use algebra and/or geometry in their jobs, students don’t need to learn these subjects.

As a high school student, I strongly disagree.

The point of learning is to understand the world. If the only point of learning is job preparation, why should students learn history, or read Shakespeare?

And while your job may never require you to know the difference between a postulate and a theorem, it will almost certainly require other math-based skills, like how to prove something or how to understand a graph.

And my surprise turned to delight when I realized that the author is a 9th grader in my Geometry class!

While her love of mathematics and her wonderful attitude toward learning certainly predate my Geometry course, I am very proud to see reflections of our classroom in her letter.

You can read the full text of her letter here.

Related Posts

By MrHonner, 9 years9 years ago

Resources Student Work Teaching Technology

Student Desmos Projects

Desmos, the free, browser-based graphing utility, has quickly become an indispensable tool in the mathematics classroom. It provides easy, intuitive access to graphs of functions and relations, and creates unique opportunities to understand mathematical relationships dynamically.

But to me, its greatest virtue may be that Desmos provides opportunities to use mathematics to create. I like to think of Desmos as a mathematical makerspace, where the tools at our disposal are exactly the tools of mathematics.

To that end, when I introduce students to Desmos, we always work toward the creation of something mathematical. Below are some beautiful examples of student work from our latest round of Desmos projects.


Varignon’s Theorem	Vector Projections


Angle Bisector Theorem	Three Lines Intersecting

You can find more of my work with Desmos here.

By MrHonner, 9 years9 years ago

Follow Mr Honner