A beautiful sculpture and a beautiful blue sky in front of San Francisco’s Exploratorium. I wonder if the same artist was responsible for the temporary exhibit in Madison Square Park a few years ago?
Related Posts
Appreciation Art Photography
Math Photo: Lego-Linear Approximations
This replica of The Thinker at Legoland got me thinking about linear approximations.
One of the fundamental ideas in Calculus is that certain kinds of curves can be very closely approximated by straight lines. In fact, when examined closely enough, these differentiable curves are essentially indistinguishable from straight lines. This is important because lines are easy to understand and analyze, whereas curves can be very complicated.
We see this phenomenon at play in Lego sculpture. Here, The Thinker’s curves are being approximated by rectangular Legos, and beautifully so. And scale plays an important role: a larger Thinker looks better in Lego than a smaller one, because the finer the approximation, the better the fit. This is something that any child who has ever tried to make a Thinker out of handful of Legos knows this firsthand.
Related Posts
Appreciation Art Data Representation Teaching
2017 — My Year in Math
Dan Meyer recently shared a fun and telling graph describing his year in math. Inspired by Dan’s idea, and by a Math for America workshop with data visualization innovator Mona Chalabi, I created my own Year in Math entry. Though the real inspiration, I guess, came from the world events that made me want to read more books and less internet.
You can find more takes on the Year in Math theme on Twitter.
I think this could make for a fun student project. I hope the students agree!
Art Geometry Resources Student Work Teaching Technology
Using Mathematics to Create — Geogebra
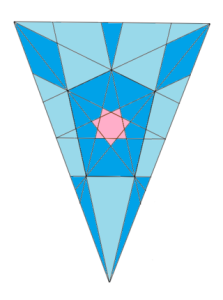One of my guiding principles as a math teacher, as I articulate in this TEDx talk, is to provide students with tools and opportunities to create with mathematics. Few things are as aligned with that principle as well as Geogebra, the free, open-source, dynamic geometry environment.
I’ve integrated a lot of Geogebra work in my Geometry class this year. I use Geogebra assignments to assess basic geometric skills, to connect old ideas to new, and to explore geometry dynamically.
But much like geometry itself, once you master a few elementary rules in Geogebra, you can create amazing and beautiful works of mathematics.
Below is an example of some wonderful student work from this year. After an introduction to polygons, students were given two simple ideas for creating new objects from polygons: constructing diagonals and extending sides. I gave students some technical tips on how to color and polish their final products, and invited them to be creative. As usual, they did not disappoint.
Students, and teachers, need more opportunities to create with mathematics. We’re fortunate to have technologies like Geogebra that offer us those opportunities.
Related Posts
- Patrick Honner’s TEDx Talk
- Curvefitting with Geogebra
- How Many Circles Pass Through Two Given Points?
Appreciation Art Numbers
Happy 2016!
In honor of the new year, here’s the complete graph on 64 vertices, with its 2016 edges!
A complete graph is a graph in which every pair of vertices is connected with an edge. In a complete graph with n vertices, there are
edges. The above graph has 64 vertices equally spaced around the perimeter. Thus, 
edges.
The number 2016 is special for a variety of reasons. For example,
So 2016 is equal to the sum of the first 63 positive integers! This makes 2016 a triangular number, a fact beautifully demonstrated by David Swart in this image.
And John D. Cook illustrates the combinatorial nature of 2016 by pointing out that this is the number of ways to place two pawns on a chessboard!
However you think of it, 2016 is a pretty great number! And here’s hoping 2016 is a great year.