Quadrilateral Challenge — A Solution
Here is one approach to answering the quadrilateral challenge posed earlier. In summary, the challenge was to prove or disprove the following statement: A quadrilateral with a pair of congruent opposite sides and a pair of congruent opposite angles is a parallelogram.
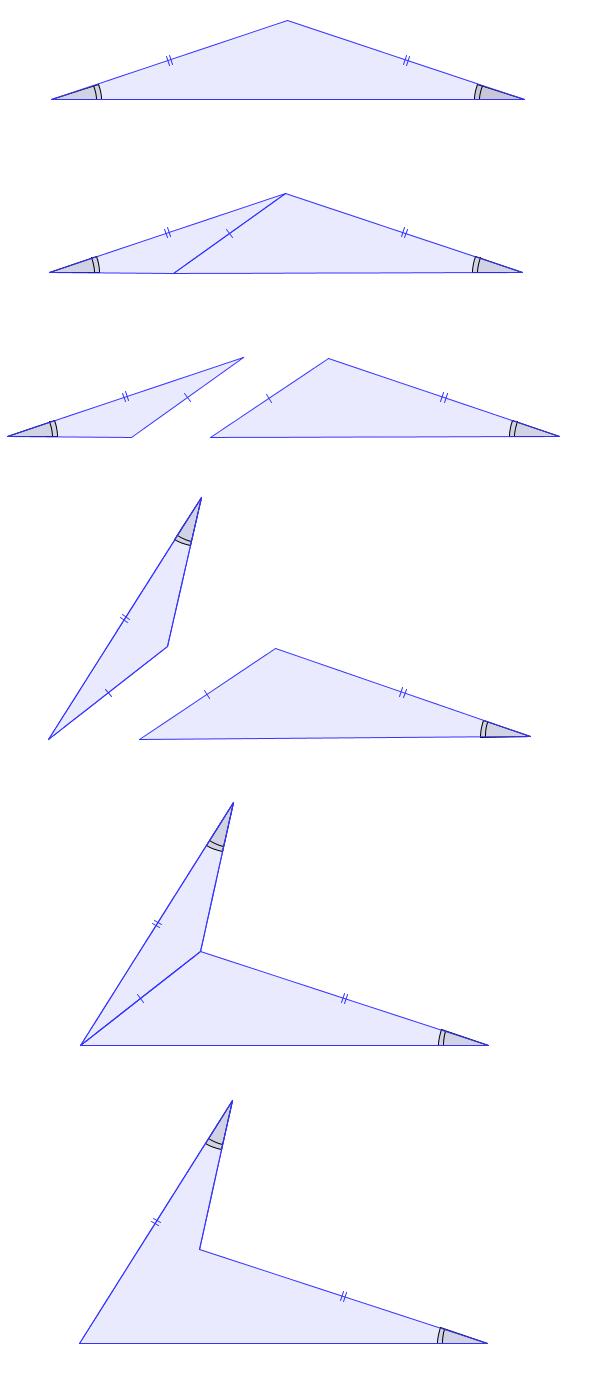
I offer this disproof without words.
By starting with an isosceles triangle, cutting it, rotating one of the pieces, and gluing it back together, we have constructed a quadrilateral with one pair of congruent opposite sides and one pair of congruent opposite angles that it is not necessarily a parallelogram!
15 Comments
Tim Ree · December 16, 2011 at 11:24 am
This a great exercise – because I can use it, I’m thinking, with my poetry unit. Do you have a sheet with those diagrams? Or did you just project the wordless proof on the board? Congruent angles are words, the area of triangles the form and content of the poem, and the syntax is the one variable that determines meaning… something… some parallel…
MrHonner · December 16, 2011 at 4:54 pm
I like your idea, what I understand of it, anyway. I’ll gladly provide you a copy of the diagrams if you can further elucidate your theory of geometric poetry.
JBL · December 19, 2011 at 2:56 pm
I haven’t read it yet, but I just found an article that might be of interest: “Is (some) mathematics poetry?” in the Journal of Humanistic Mathematics http://scholarship.claremont.edu/jhm/vol1/iss1/7/
NA · December 17, 2011 at 4:44 pm
I would love to see this in class, Mr. Ree! 🙂
MrHonner · December 20, 2011 at 4:43 pm
Thanks for the article, JBL! I’ve passed it along; it’s a quick, amusing read.
JBL · December 16, 2011 at 12:19 pm
And, to tie this in to my comment on the previous thread, cutting an isosceles triangle by a cevian is exactly how you get a pair of noncongruent triangles that are related by SSA.
MrHonner · December 16, 2011 at 4:58 pm
Yes. I love the appearance of the Law of Sines ambiguous case here. This also offers another explanation as to why, if the opposite congruent angles are right, you can prove it’s a parallelogram.
JBL · December 17, 2011 at 7:15 pm
Nice; I had been wondering whether there was a “good” reason that right angles had that property (and equivalently why SSA *is* a congruence relation for right triangles); tying in the Law of Sines and the ambiguity of arcsin is a nice way to make the connection.
Somewhat further afield, this also settles the question of whether such a quadrilateral can be cyclic: if so, the opposite equal angles must be right, whence we’re stuck with just rectangles.
moukaouame · December 16, 2011 at 4:46 pm
Il faut rajouter la convexité.
MrHonner · December 16, 2011 at 4:56 pm
My French isn’t so good: are you suggesting that we add the requirement of convexity to the quadrilateral to eliminate this counterexample?
JBL · December 17, 2011 at 12:14 am
Yes, that’s the suggestion. But it doesn’t eliminate all counter-examples: you happened to choose an example that involves gluing two obtuse angles together, but it’s easy enough not to. For example, if you cut an equilateral triangle with a cevian that trisects one side and apply this operation, the resulting quadrilateral is convex.
MrHonner · December 17, 2011 at 2:46 pm
Nice example. You inspired me to cut up some equilateral triangles and explore!
Yelena Weinstein · December 18, 2011 at 9:06 pm
Yes! That’s what I was trying to draw on the board in MfA! But it’s a cool and convincing way.
Derek Pipkorn · January 7, 2015 at 9:13 am
Showed this to my Honors Geometry class. A couple of simple questions came up: “What is the definition of an opposite side? What is the definition of an opposite angle?” This figure didn’t fit their previous knowledge of those terms.
MrHonner · January 7, 2015 at 8:14 pm
Yes, we had some similar conversations. What’s nice is that in a quadrilateral you can temporarily solve the problem by contrasting “opposite” with “adjacent”, and then immediately re-introduce the problem by asking the student to find the “opposite” side in a pentagon!