Are These Tests Any Good? Part 5

This is the fifth entry in a series examining the 2011 NY State Math Regents exams.  The basic premise of the series is this:  if the tests that students take are ill-conceived, poorly constructed, and erroneous, how can they be used to evaluate teacher and student performance?

In this series, I’ve looked at mathematically erroneous questions, ill-conceived questions, under-represented topics, and what is perhaps the worst question in Regents history.  In this entry, I’ll use questions from two exams to discuss duplication, lowered-expectations, and poor test construction.

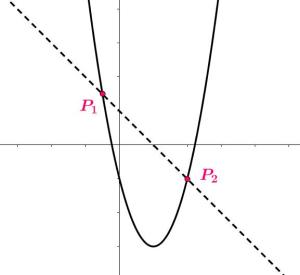
Number 37 from the 2011 Geometry Regents exam is a 4-point question which asks students to solve the following system of equations graphically:

Number 39 from the 2011 Algebra 2 / Trigonometry Regents exam is a 6-point question which asks students to solve the following system of equations algebraically:

These two systems of equations are roughly equivalent in terms of difficulty.  Why is a question suitable for the Geometry exam appearing on a the Alg 2/Trig exam, and as the highest-valued question (6 points) to boot?  In New York state, the Alg 2/Trig course follows Geometry in the standard sequence, so it is strange to see the same kind of problem on two state exams that are designed to be taken at least a year apart.

It’s true that the Alg 2/Trig test question asks for an algebraic solution, as opposed to a geometric solution, but that is essentially the only difference between the two.  This being the case, this speaks to a serious problem in how these tests are conceived and designed.

Looking at these two tests, one might conclude that learning to solve this kind of system algebraically is an important part of the Alg 2/Trig course:  why else would the official exit exam require the use of this technique in solving a problem that could have been solved last year?

Solving systems algebraically is definitely is a fundamental skill; so fundamental, in fact, that it is part of the Integrated Algebra curriculum (see the Integrated Algebra Pacing guide on the official schools.nyc.gov website).  Integrated Algebra is the course students take before they take Geometry!  Since many students take IA in 9th grade and take Alg 2/Trig in 11th or 12th grade, this means that a 6-point question on the Alg 2/Trig exam is testing the student’s ability to solve a problem they should have been able to solve two math courses ago.

Students should be able to solve this kind of problem at all mathematical levels, but why is material from two courses ago playing such a prominent role on an advanced exit exam?  What Alg 2/Trig course material is being shortchanged in order to re-test more elementary skills?  And to the point, how can this be considered a legitimate assessment of what a student learned in an Alg 2/Trig course?

Furthermore, in each case the scoring guide allows for half credit if the problem is solved using a method different than the one specified.  This is a reasonable policy, but what then is the purpose of a question specifically designed to test knowledge of a technique?  On the Alg 2/Trig test, a student can earn half credit for solving the system graphically; that means a student can get 3 of the 6 points by simply doing exactly what they did on the same problem on last year’s Geometry exam.

This example highlights how some questions on these exams aren’t directly connected to the content of their respective courses.  If a test isn’t legitimately designed around the curricula and content of the course, how can teachers and students effectively prepare?  How could such tests be valid assessments of what a student learns in that class?  Or how effectively a teacher teaches?  These are all questions that aren’t asked enough in the debate about standardized tests, student performance, and teacher accountability.

Related Posts

• Regents Recaps
• Regents Recap — June 2016: How Much Should This Be Worth?