Are These Tests Any Good? Part 3
This is the third entry in a series examining the 2011 NY State Math Regents exams. The basic premise of the series is this: if the tests that students take are ill-conceived, poorly constructed, and erroneous, how can they be used to evaluate teacher and student performance?
In Part 1, I looked at several questions that demonstrated a significant lack of mathematical understanding on the part of the exam writers. In Part 2, I looked at several poorly constructed questions that were vague, incoherent, or tested irrelevant material. Here, in Part 3, I’ll look at a single question that highlights problems with the scope of the exams.
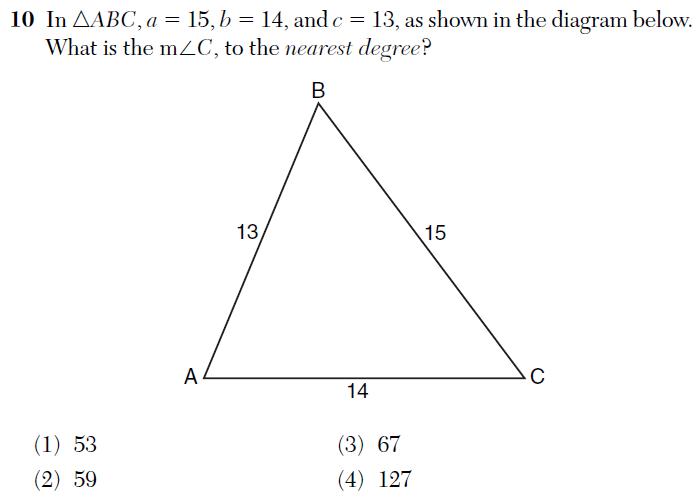
This is number 10 from the 2011 Algebra 2 / Trigonometry Regents exam: given the three sides of a triangle, find the measure of one of the angles.
There is nothing wrong with this question. It’s clear and unambiguous. It connects to a fundamental idea in trigonometry, that knowing three pieces of information is often enough to determine everything about that triangle. And the question is designed to test the student’s knowledge of a fundamental skill in trigonometry: applying the Law of Cosines.
The problem here is that this is only question on this exam related to these topics. This two-point, multiple choice question is the only place on this Trigonometry exam that requires the use of either the Law of Cosines or the Law of Sines.
Perhaps there is a useful discussion to be had about just how important the Laws of Sines and Cosines are. To me, mastery of these theorems is one of the clear end-goals of a trigonometry course. Trigonometry literally means “measure of triangles”, and these two theorems represent the culmination of our knowledge about measuring triangles. Therefore, they should be featured more prominently in a final assessment.
It’s reasonable to debate just how prominently they should be featured, but it’s hard to imagine any trigonometry teacher agreeing that, based on their relative importance, two points out of 88 is a reasonable representation.
Furthermore, a debate about the relative importance of these particular theorems becomes less meaningful when you realize what, instead, appears on this exam. A rough estimate suggests that 12-14 points on this test deal with quadratic functions, a topic from Algebra 1. That’s 15% of the exam. In fact, a review of the entire test suggests that 34-36 of the points relate to topics that should be taught in an introductory Algebra course; that’s nearly 40% of the exam. Why are we testing 9th grade material on an 11/12th grade Regents Exam? That’s probably a topic for another day.
Related Posts
0 Comments