Are These Tests Any Good? Part 2
This is the second entry in a series that examines the test quality of the New York State Math Regents Exams. In the on-going debate about using student test scores to evaluate teachers (and schools, and the students themselves), the issue of test quality rarely comes up. And the issue is crucial: if the tests are ill-conceived, poorly constructed, and erroneous, how legitimate can they be as measures of teaching and learning?
In Part 1 of this series I looked at three questions that demonstrated a significant lack of mathematical understanding on the part of the exam writers. Here, in Part 2, I will look at three examples of poorly designed questions.
The first is from the 2011 Integrated Algebra Regents: how many different ways can five books be arranged on a shelf?
This simple question looks innocent enough, and I imagine most students would get it “right”. Unfortunately, they’ll get it “right,” not by answering the question that’s been posed, but by answering the question the exam writers meant to ask.
How many different ways are there to arrange five books on a shelf? A lot. You can stack them vertically, horizontally, diagonally. You can put them in different orders; you can have the spines facing out, or in. You could stand them up like little tents. You could arrange each book in a different way. The correct answer to this question is probably “as many ways as you could possibly imagine”. In fact, exploring this question in an open-ended, creative way might actually be fun, and mathematically compelling to boot.
But students are trained to turn off their creativity and give the answer that the tester wants to hear. A skilled test-taker sees “How many ways can five books be arranged on a shelf?” and translates it into “If I ignore everything I know about books and bookshelves, stand all the books upright in the normal way, don’t rotate, turn or otherwise deviate from how books in math problems are supposed to behave, then how many ways can I arrange them?”
This question is only partly assessing the student’s ability to identify and count permutations. This question mostly tests whether the student understands what “normal” math problems are supposed to look like.
This problem is an ineffective assessment tool, but there’s something even worse about it. Problems like this, of which there are many, teach students a terrible lesson: thinking creatively will get you into trouble. This is not something we want to be teaching.
Here’s a question from the 2011 Algebra II and Trigonometry exam:
Solving equations is one of the most important skills in math, and this question pertains to a particular method (completing the square) used to solve a particular kind of equation (quadratic). But instead of simply asking the student to solve the problem using this method, the question asks something like “if this procedure is executed normally, what number will be written down in step four?”.
This is not testing the student’s ability to do math; instead, it’s testing whether or not they understand what “normal” math looks like. There are many ways to solve equations, and there are many ways a student might use this method. Whether it looks exactly like what the teacher did, or what the book did, isn’t especially relevant. So why is that being tested? And like the question above, this reinforces the idea that thinking creatively can be dangerous by insisting that students see the “normal” solution as the only correct one.
Finally, here’s a problem from the 2011 Geometry Regents:
Once again, the student is not being tested on their knowledge of a concept or on their ability to perform a task. Instead, they’re being tested on whether or not they recognize what “normal” math looks like, and that’s just not something worth testing. There are lots of legitimate ways to construct a perpendicular bisector: why are we testing whether the student recognizes if the “normal” way has been used?
These three problems showcase some of the dangers inherent in standardized testing. Questions like these, and the tests built from them, discourage creative thinking; they send students the message that there is only one right way to do things; they reinforce the idea that the “correct” answer is whatever the tester, or teacher, wants to hear; and they de-emphasize real skills and understanding.
At their worst, these tests may not just be poor measures of real learning and teaching; they may actually be an obstacle to real learning and teaching.
Related Posts
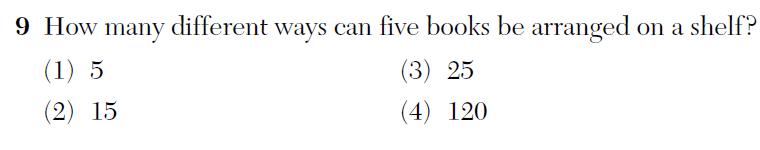
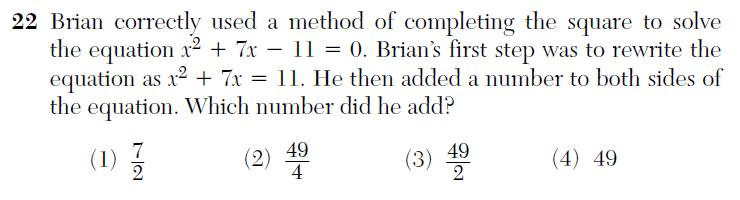

5 Comments
Allison Krasnow · August 18, 2011 at 2:04 pm
I so agree with you. A related concern is why are we testing similar content in the exact same way in multiple courses. Your #22 Algebra 2/Trig question could have been taken verbatim from the California Standards Test for Algebra 1. Between 4th-7th grade, traditional textbooks feel to me like they’re about 85% similar. I can’t figure out who in the education world can justify this as sound pedagogy.
MrHonner · August 18, 2011 at 3:12 pm
We definitely have curriculum problems in New York, too, and they manifest themselves on these exams. It’s not duplication or overlap; it’s the classic mile-wide, inch-deep problem (at least at the high school level; I’m not familiar with MS curricula). And as has been pointed out before, with so many topics to test on, you can end up with an Alg/Trig exam that considers the Law of Sines to be of equal importance as using a calculator to find the r-value of a regression line.
The high level problems aren’t surprising to me, I guess because of the politics and bureaucracy surrounding education. It’s these bad questions that I don’t get. Unclear directives, testing irrelevant aspects of a problems, flat-out mathematical errors. It happens consistently, and nothing really changes. And it’s disturbing that we as teachers are judged on how students navigate all of this.
Kate Nowak · August 19, 2011 at 11:17 am
Oh, but, we do have duplication and overlap! For example, center-radius form of the equation of a circle is fair game on ALL THREE MATH REGENTS EXAMS. Also, if I’m remembering correctly, last June students had to solve a quadratic-linear system by graphing on both the IA and the Geometry exams.
MrHonner · August 19, 2011 at 11:37 am
I don’t mind that systems of equations appear on multiple exams–I’d say solving systems is a fundamental mathematical skill that should come up in every course.
How those systems appear on the tests, however, is another matter. As you know, essentially identical systems-of-equations problems appeared on this year’s Geometry and Alg/Trig exams, and the only difference was the requirement that the first be solved graphically and the second be solved algebraically. And frankly, students should be able to solve such problems both ways by the end of a first-year algebra course.
But to me, this is a reflection of poor test design, not unnecessary curriculum overlap. The curricula have lots of problems, but overlap wouldn’t be at the top of my list.
JBL · August 20, 2011 at 11:32 am
Christ that third one is awful. JD2718 mentioned this one, too: “The diagonals of a quadrilateral are congruent but do not bisect each other. The quadrilateral is:” with four answer choices. Oy vey.