Regents Recap, August 2017: How Do You Explain that Two Things are Equal?
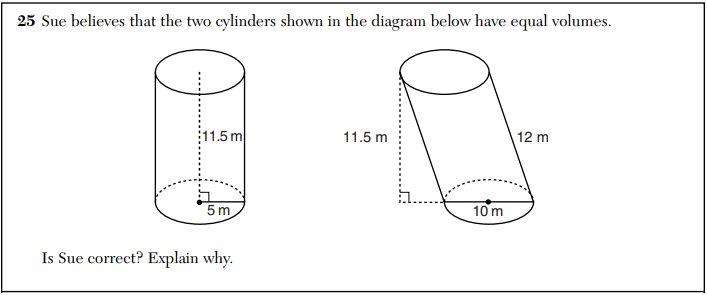
Sue believes these two cylinders from the August, 2017 New York Regents Geometry exam have equal volumes. Is Sue correct? Explain why.
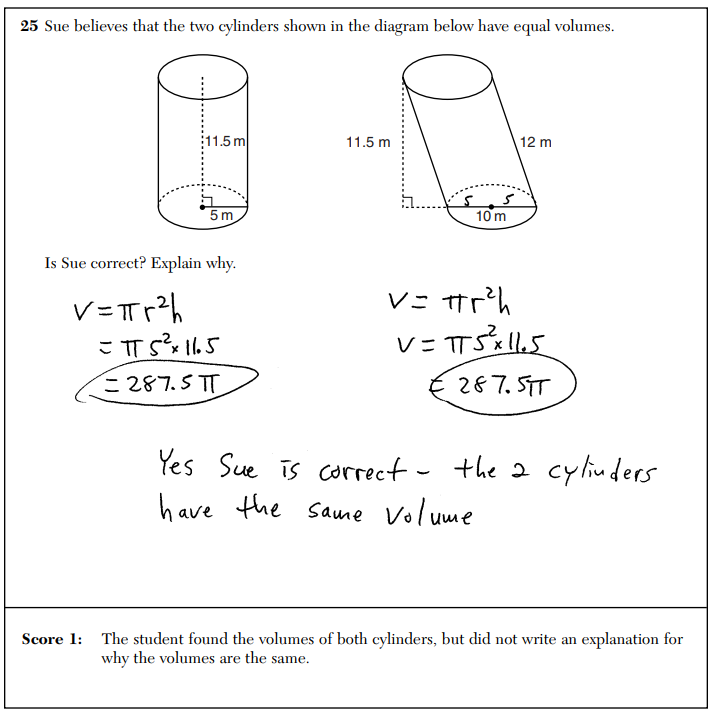
Yes, Sue, you are correct: the two cylinders have equal volumes. I computed both volumes and clearly indicated that they are the same. Take a look!
Wait. Why did I only get half-credit? What’s the problem, Sue? You don’t think this is an “explanation”? The two volumes are equal. The explanation for why they are equal is that I computed both volumes and got the same number. I don’t know of any better explanation for two things being equal than that.
What’s that? You wanted me to say “Cavalieri’s Principle”? But if I compute the two volumes and show that they are equal, why would I need to say they are equal because of some other reason? Oh, never mind, Sue. See you in Algebra 2.
Related Posts
7 Comments
John Golden · September 14, 2017 at 9:35 am
Of all the Regents Follies you share, the inexplicable grading policies on constructed response drive me the most crazy. Gaaah!
MrHonner · September 14, 2017 at 7:46 pm
Setting aside the sheer absurdity of it, there are real consequences.
For schools that are allowed to grade their own Regents exams–charter schools, for example, and schools outside of NYC–I bet most teachers grading this exam would look at this model response, say “This is completely idiotic”, and give such a response full credit. But for schools in NYC, where grading is done off-site at pooled grading centers, the site administrators are much more likely to adhere strictly to these model response sets. The consequence of this would be lower scores for NYC public school students.
Anon · September 14, 2017 at 7:48 pm
This is honestly incredible.
Math Teacher · September 24, 2017 at 11:28 am
I teach at a charter school, and we definitely thought this sample scoring was ridiculous but we followed the rubric and guidelines when scoring. We do not veer from the model response sets even if we disagree with them. There is plenty of reason to be upset about the scoring of this question, but assuming that this grading affects public schools disproportionately in comparison to charter schools is not one of them.
MrHonner · September 24, 2017 at 3:26 pm
Thanks for your comment. I’ll remain appropriately suspicious. Of course, some data transparency would easily settle the matter, but I don’t see that happening.
MrHonner · September 24, 2017 at 6:11 pm
And by “I’ll remain appropriately suspicious”, I mean of the situation in general, certainly not of you and school. Sorry that wasn’t clear in my original response.
Common Sense · December 22, 2017 at 7:24 pm
The way this problem is presented to students is ambiguous. Description does not inform student that the base of inclined cylinder is circle. On the other hand, common sense would tell you that cross-section of cylinder is ellipse. The size 10 m on picture shows only on major axis of that ellipse. Obviously, it is not enough to calculate area of the base, but it is enough to judge that area of base will be less than area of a circle with diameter 10 m. Therefore inclined cylinder has smaller volume. The answer should be “Sue is wrong”.