Regents Recap — June, 2016: Simplest Form

“Simplest form” is a dangerous phrase in math class.  Whether a form of an expression is simple or not depends on context.  For example, while and are representations of the same number, the first fraction is likely to be seen as simpler than the second.  But if the goal were, say, to determine if the number was greater than , then the expression on the right might be considered simpler.

Despite the wide and varied uses of the phrase “simplest form”, I have never heard it used in the context of complex numbers.  So I was surprised by this Common Core Algebra 2 Regents exam question.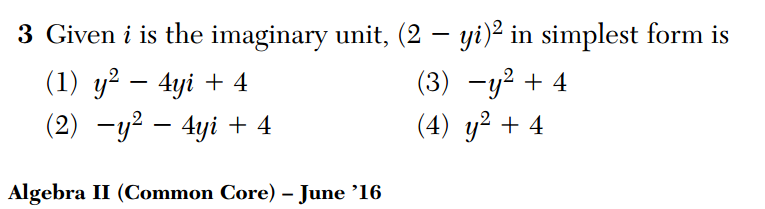

I don’t know what the author of this question means here by “simplest form”.  I asked around, and someone suggested that the natural interpretation of “simplest form” here is a + bi.  That seems reasonable, but since none of the answers are in a + bi form, the author of this question could not have meant that.  [It is also worth noting the implicit assumption here that y is a real number, an issue that has come up before on these exams].

What’s most bothersome about this imprecise use of language is that it is completely irrelevant to this question.  Whatever “simplest form” means here, it is of no consequence:  there is no answer choice which is otherwise correct but in some improper form.

The question should simply ask which expression is equivalent to the given expression.  The use of “simplest form” here not only obfuscates the mathematics of the problem, but models imprecise use of mathematical terminology.  We should expect our high stakes exams to do better.

Related Posts

• Regents Recaps
• Regents Recap — June, 2012: Erroneous Questions
• Regents Recap — June, 2013: Encouraging Bad Habits