Regents Recap — January 2015: Admitting Mistakes
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
This is question 27 from the Geometry exam.
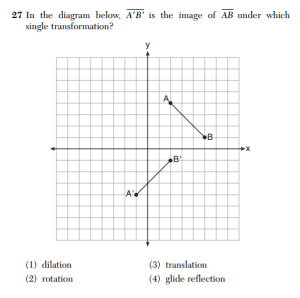This question has two correct answers: it is possible to map AB onto A’B’ using a glide reflection or a rotation. The original answer key indicated that (4) glide reflection was the correct answer. After the exam was administered, the state Department of Education issued a correction and told scorers to award full credit for both (2) and (4).
Mistakes happen, even on important exams that many people work hard to produce. But when mistakes are made, those responsible should accept responsibility, not equivocate.
Here’s the official correction from the state.
It’s hard to accept that the issue here was a lack of specificity in the wording of the question. The issue is that someone wrote a question without fully thinking through the mathematics, and then those tasked with checking the problem also failed to fully think through the mathematics. This isn’t a failure in communication; this is a failure in management and oversight.
And it has happened before. This example is particularly troubling, in which those responsible for producing these exams try to pretend that an egregious mathematical error is really just a lack of agreement about notation. Sometimes errors are just erased from the record with little or no explanation, and then, of course, there are the many mistakes that are never even acknowledged.
Mistakes are bound to happen. But by pretending that substantial errors are just misunderstandings, differences of opinion, or typos, the credibility of those responsible for these high-stakes exams suffers even further damage.
5 Comments
Joshua Greene · March 27, 2015 at 11:26 am
Maybe a fun salvage for this question (using it to benefit our and students’ mathematical understanding, not excusing the test management):
Under what circumstance, if any, are two line segments of equal length not images of each other under rotation? In which of those cases, if any, are the two line segments images of each other under glide reflection?
Your series has prompted me to tweet another question: are there any standardized tests you would encourage someone to take voluntarily? In other words, if I’m a student from another jurisdiction/school district/whatever, the test has enough educational value that I should make an effort to take it.
Conjecture (weak form): none in the US
Conjecture (strong form): none globally
If you want, we could include math contests in the scope of this question. personally, I’m conflicted about how to modify the conjectures in this broader scope.
MrHonner · March 27, 2015 at 11:44 am
I have a similar salvage in mind. I’ll share in a future post, and add a link to your suggestion, as well.
And I answered “AMC” to your question on Twitter. I think test-makers could learn a lot by studying how good math contests are built and used.
Amy Hogan · March 28, 2015 at 10:21 am
Don’t forget about the multiple choice question on the Jan. 2012 Regents in which the question had no correct answer: https://mrhonner.com/archives/7223.
pasmith · March 30, 2015 at 3:39 pm
It depends how you define “rotation”. Certainly a composition of a pure rotation and a translation will do it. However the only possible center of a pure rotation taking AB to A’B’ is the intersection of the continuations of those line segments, and that intersection is not equidistant from B and B’. Thus it cannot be done by a pure rotation.
That there is ambiguity about whether “rotation” means “pure rotation” or “a composition of a pure rotation and a translation” is evident from the question posed by Joshua Greene, which is otiose if non-pure rotations are included: you can always purely rotate one line segment to be parallel to the other and then translate it.
MrHonner · March 30, 2015 at 3:49 pm
There are, in fact, two rotations that map AB onto A’B’, and neither of them are centered at the intersection of lines AB and A’B’.