Regents Recap — June 2014: Lack of Scale
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
The following question appeared on the June, 2014 Algebra 2 / Trig exam.
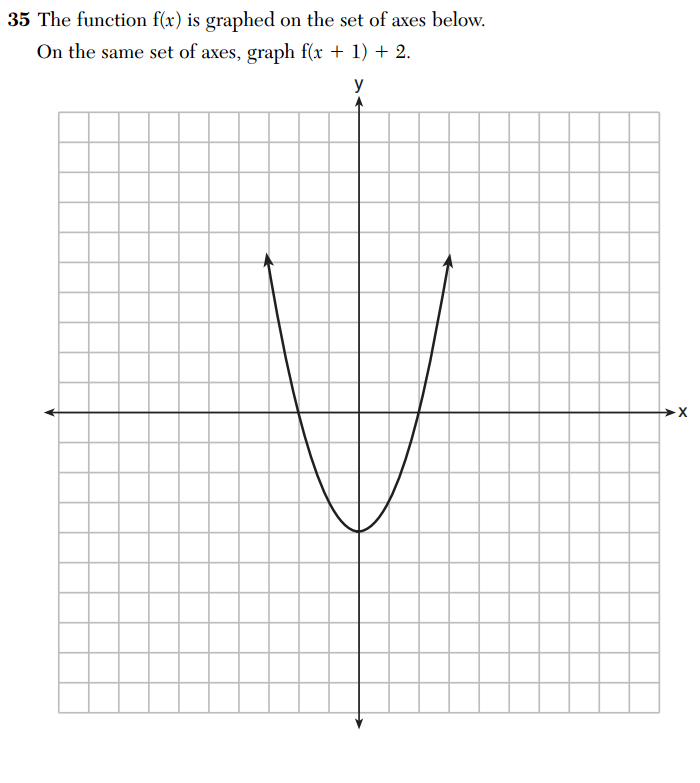Graphs without scales are common on Regents exams (I’ve written about this before). Personally, it’s not a huge deal to me–I’m a lazy grapher, myself. However, a colleague of mine regularly complains about this, and she made an excellent point regarding the grading of this particular problem.
The solution to this problem involves translating the graph one-unit to the left and two units up. But since no scale is given on the graph, it’s not clear what one unit to the left would be. If we assume the box on the graph indicates one unit, then the red graph below would be appropriate. But if we assume a box to represent half-a-unit, the purple graph would be correct.
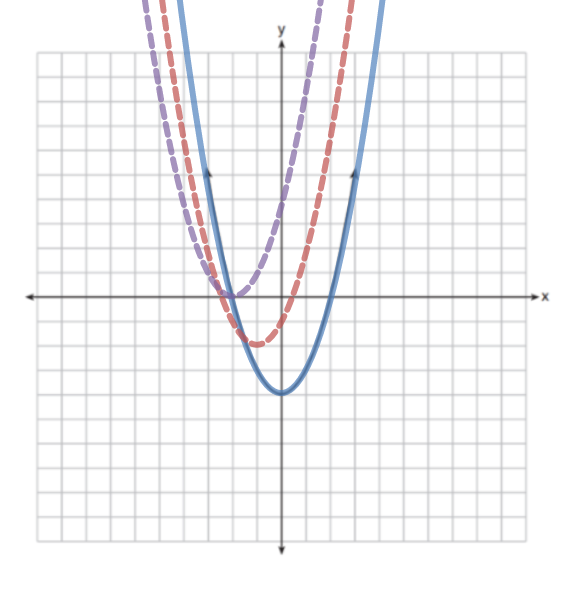If no scale is explicitly given, it seems like both graphs should be considered correct and receive full credit. But the rubric doesn’t address this possibility, and it’s unlikely students were given the benefit of the doubt.
3 Comments
Jonathan · August 31, 2014 at 10:01 am
I am as critical of the Regents as anyone else, maybe more. And they certainly SHOULD indicate units. But in this case, lacking crucial information, the only reasonable assumptions are that each small box is one unit square, or (less reasonably) that the drawn portion of each quadrant is one unit square.
A kid who assumed each box was half a unit? Yeah, they should have gotten credit. And a talking to.
MrHonner · August 31, 2014 at 10:09 am
The claim that those are the only reasonable assumptions is a strong one, but I doubt I’d try very hard to dispute it.
The real issue here is that the act of making such assumptions is rarely, if ever, discussed with students. Student use different scales all the time on graphs; a tick could mean a half, or a quarter, or a fifth. If they don’t go into a problem thinking “What is the unit here?”, then they may just end up defaulting to something for no particular reason. And then getting the question wrong.
A theme in my extensive critiques of these exams is that students should not be asked to guess what the exam-writer is thinking. The student has enough to worry about.
Priscilla Bremser · August 31, 2014 at 12:40 pm
Whether we intend it or not, any assessment (formative or summative, high or low stakes) conveys messages to the student as well as to the assessor. This item suggests that it’s not important to indicate scale on a graph. As you indicated in an earlier post, test writers should model the practices we hope our students will adopt. CCSS MP#6 – Attend to precision – has been neglected here.
Thank you for taking the time to look closely at the latest New York State exams. I wonder what other messages students might get from them about mathematics content and practice. Many of my (college) students arrive with a pretty firm idea that mathematics is only about getting the right answer, and getting it fast. It’s not hard to figure out where that came from.