Regents Recap — June 2013: Another Embarrassment
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
Sometimes a poorly-written question together with an ill-conceived scoring rubric creates a truly embarrassing situation for those involved with the New York math Regents exams.
Consider the following question from the June 2013 Geometry exam.
This two-point problem seems straightforward enough, but things take a turn in the scoring rubric.
According to the rubric, the only way a student can earn full credit here is to graph both loci. Unfortunately, the student was only asked to graph one locus.
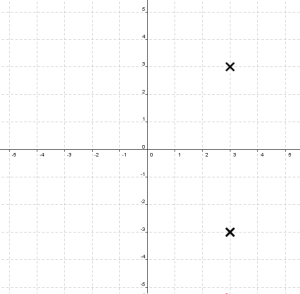
The problem directs students to graph the set of points that are both four units from the x-axis and equidistant from the two given points. This is a single, compound locus. Only two points satisfy both conditions simultaneously, so the graph of the locus looks like this:
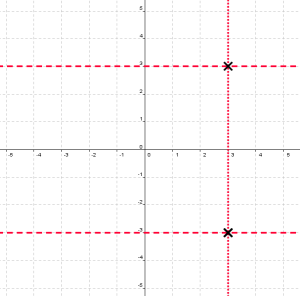
Unfortunately, if a student graphs only the locus they were asked to graph, the rubric awards them a maximum of one out of two points. Why? Because the rubric mistakenly interprets this compound locus as two loci: the set of points that are four units from the x-axis and the set of points that are equidistant from (-2,0) and (8,0). The graph of these two loci look like this:
The correct compound locus is the intersection of these two loci. But the students were only asked to graph the points that satisfy both conditions; not the points that satisfy either condition. It’s absurd to penalize students for not providing information that wasn’t asked for.
I brought this to the attention of our grading site supervisor, but nothing was done. The site supervisor ultimately defended the rubric by claiming the graphs of the two loci constituted appropriate work, and so were necessary for full credit. But this ad hoc argument barely warrants a response. Someone here wrote a bad question, a bad rubric, or both. Mistakes happen, but in the world of high-stakes testing, students and teachers end up paying the price, while the test-makers avoid accountability.
Other math teachers I spoke to had similar experiences at their grading sites. And unfortunately, this isn’t the first time state administrators were reluctant to address an absurdly erroneous question.


2 Comments
Willie Wong · August 21, 2013 at 3:26 am
It took me a really long time to figure out what you are complaining about. So just to make sure I am understanding it right: implicitly in the rubrics the two loci are (a) the points that are 4 units from the x axis and (b) the points that are equidistant from the two given points.
And you are complainig that those students who graphed only the locus of points that is the intersection of (a) and (b) will get only partial credit?
MrHonner · August 21, 2013 at 7:14 am
Willie-
Sorry if I wasn’t clear enough. I’ve added some graphs to help explain the issue.
Yes, you are correct. If students only graph the intersection of the two individual loci, they receive partial credit. The complaint, of course, is that the intersection of these two loci is all they were asked to graph: the problem asks for the graph of a compound locus, not graphs of the individual loci.