Regents Recap — June 2013: Encouraging Bad Habits
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
Some of the worst exam questions aren’t merely erroneous, but actually encourage students to exercise bad mathematical habits. Consider these questions from the June 2013 Algebra 2 / Trig exam.
Notice that the problem doesn’t specify what kind of series this is: the student is expected to assume that the series is geometric. This is a terrible habit to encourage, and I wrote about this the last time it happened on a Regents exam. I guess no one is listening.
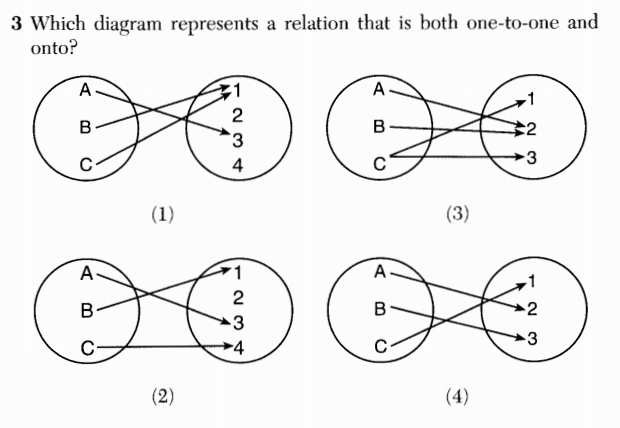
In order to determine whether a relation is one-to-one or onto, it is necessary to know the relation’s domain and range. Here, the student is expected to assume that the oval on the left represents the domain of the relation and the oval on the right represents the range. Perhaps these assumptions are reasonable given the nature of the diagrams, but this just seems sloppy to me. I wouldn’t accept imprecise formulations of functions and relations like this from my students; I would demand they be more explicit. (It’s also worth noting that the relation in (2) is one-to-one and onto its image in the right-hand oval.)
Here’s another example of sloppiness in question construction.
Is it supposed to be obvious that the i here is the imaginary unit? The letter i could be just a variable, like, say, the m that also appears in the question. The available answers support the assumption that , but why are we forcing students to play test-detective?
The Regents exams also continue with their long-standing tradition of presenting unscaled graphs, another bad mathematical habit to encourage.
I believe these tests should stand as exemplars of proper mathematics. Maybe I’m alone in thinking this, but it seems to me that repeated exposure to these sloppy exam questions might actually interfere with a student’s ability to truly understand the underlying mathematics.
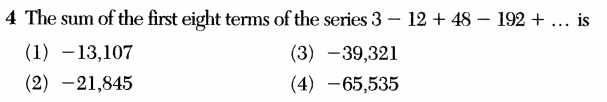
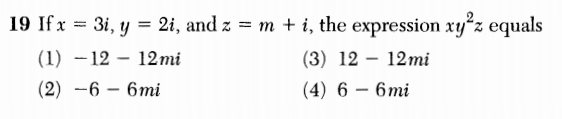
3 Comments
Mike Lawler · July 24, 2013 at 9:24 am
I think you mean “geometric” not “arithmetic” in the description of the first problem.
MrHonner · July 24, 2013 at 9:53 am
Yes. Thanks for spotting the error. I guess I’ve been looking at these tests so long now I’m assuming all series are arithmetic!
Evelyn Lamb · July 25, 2013 at 5:49 pm
Those “next term of the series” type questions have always driven me nuts. What if it’s the series 3 -12 +48 -192 +7 billion…?!